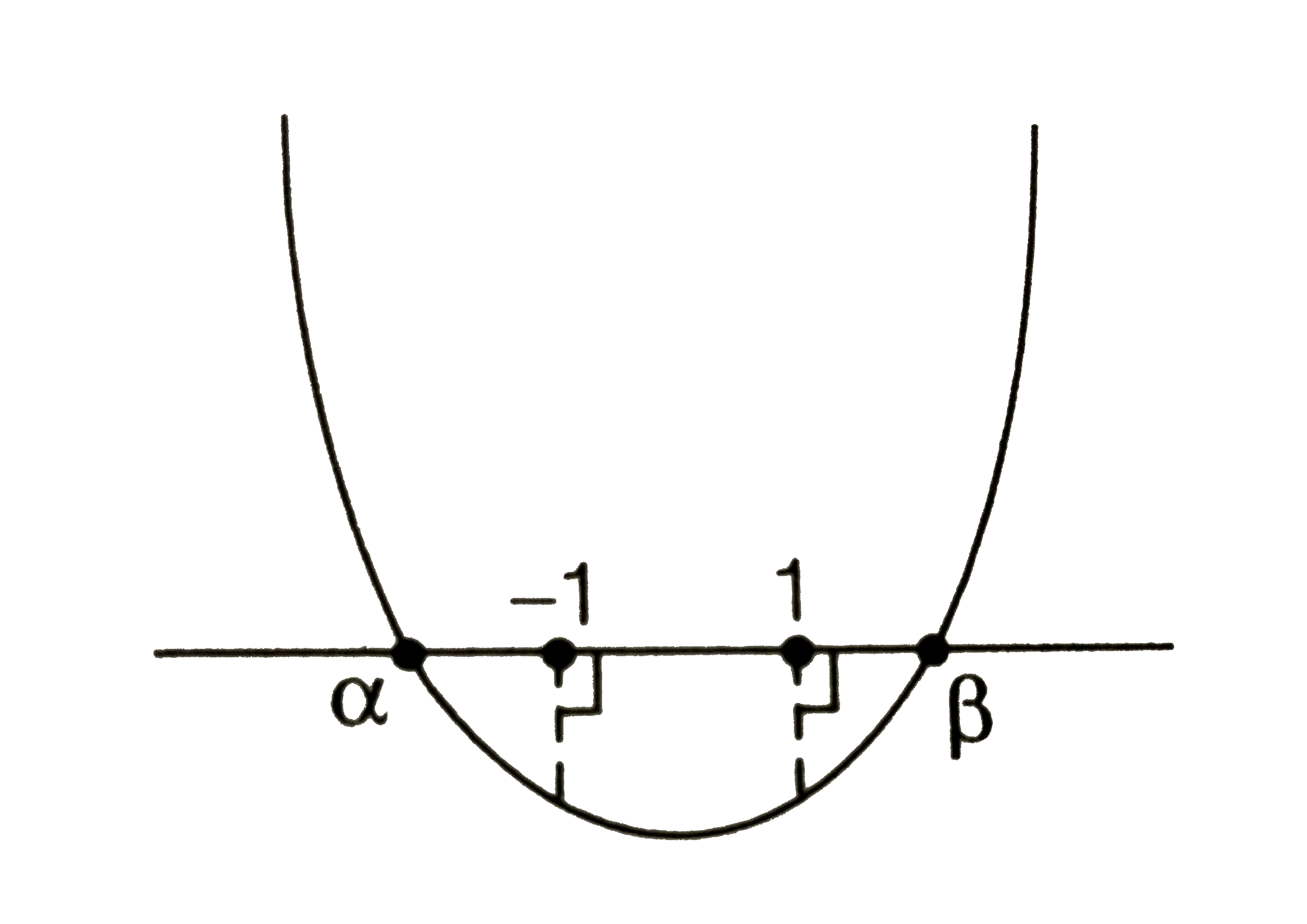
Let a, b, c be real. If has two real roots and such that and , then is Solution in Kannada
Since and
and
Now
[if ]
and [if ]
or
On both cases
Aliter
Let
and
and
Then
Similar Questions
Let a, b, c be real, if ax2+bx+c=0 has two real roots α,β, where a<−1andβ>1, then the value of 1+ca+∣∣∣ba∣∣∣ is :
View SolutionIf a, b, c are real if ax2+bx+c=0 has two real roots α,β where a<−1,β>1 then
View SolutionShow that a2x−α+b2x−β+c2x−γ−x+δ=0 has only real roots if a,b,c,α,β,γ,δ are all real .
View SolutionLet a, b, c ∈R be such that a + b + c <0,a−b+c<0andc>0. If αandβ are roots of the equation ax2+bx+c=0 , then value of [α]+[β] is
View SolutionIf α,β re the roots of ax2+c=bx, then the equation (a+cy)2=b2y in y has the roots a.αβ−1,α−1β b. α−2,β−2 c. α−1,β−1 d. α2,β2
View SolutionLet a, b, c be real. If ax2+bx+c=0 has two real roots α and β such that α<−1 and β>1, then 1+ca+∣∣∣ba∣∣∣is
View SolutionLet a,b,c be real. If ax2+bx+c=0 has two real roots α,β where α<−1 and β>1,then show that 1+ca+∣∣∣ba∣∣∣<0.
View SolutionLet a,b,c ∈Randa>0. If the quadratic equation ax2+bx+c=0 has two real roots αandβ such that α>−1andβ>1 , then show that 1+∣∣∣ba∣∣∣+ca>0
View Solution