All the values of m for which both roots of the equation x2−2mx+(m2−1)=0 are greater than -2 but less than 4 lie in the intervalSolution in Kannada
Let f(x)=x2−2mx+x2−1, as exactly one root of f(x)=0 lies in the interval (−2,4), we can take D>0 and f(−2)f(4)<0.
(i) Consider D>0
(−2m)2−4.1(m2−1)>0⇒4>0
∴mεR……………i
(ii) Consider f(−2)f(4)<0
(4+4m+m2−1)(16−8m+m2−1)<0
⇒(m92)+4m+3)(m2−8m+15)<0
⇒(m+1)(m+3)(m−3)(m−5)<0
⇒(m+3)(m+1)(m−3)(m−5)<0
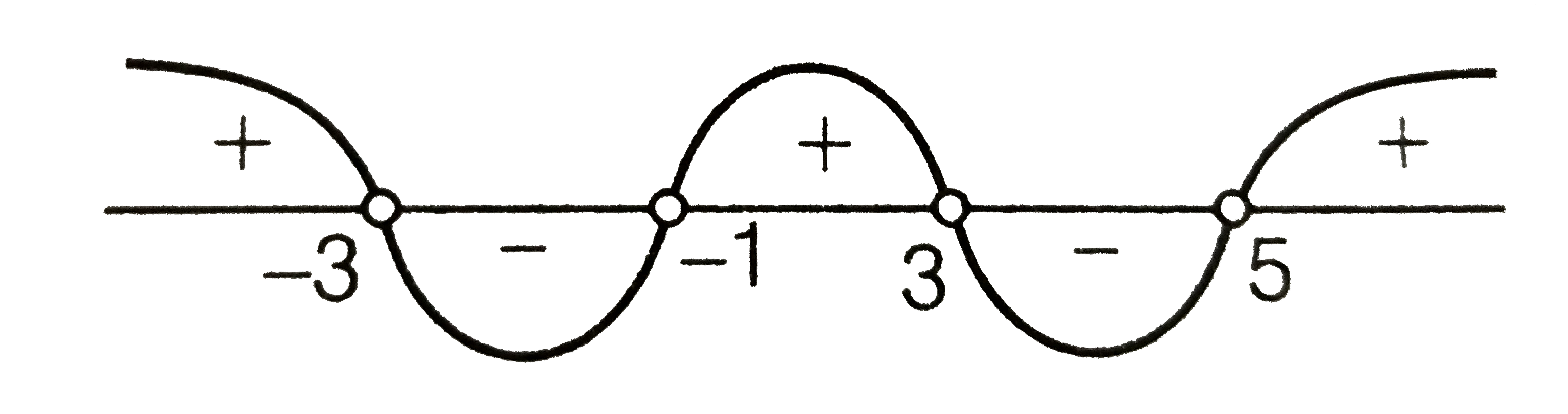
∴mε(−3,−1)∪(3,5).........ii
Hence the values fo m satisfying Eq. (i) and (ii) at the same time are mε(−3,−1)∪(3,5).
Similar Questions
m के वह सभी मान, जिसके लिये समीकरण x2−2mx+m2−1=0 के दोनों मूल -2 से बड़े परन्तु 4 से कम हो, निम्न में से किस अन्तराल में स्थित है:
(i) m>3 (ii) −1<m<3 (iii) 1<m<4 (iv) −2<m<0
View Solutionm के वह सभी मान, जिसके लिये समीकरण x2−2mx+m2−1=0 के दोनों मूल -2 से बड़े परन्तु 4 से कम हो, निम्न में से किस अन्तराल में स्थित है:
(i) m>3 (ii) −1<m<3 (iii) 1<m<4 (iv) −2<m<0
View SolutionFind the values of x for the given equation 3x2+5x−2=0
View SolutionAll the values of m for which both roots of the equation x^(2)-2 m x+(m^(2)-1)=0 are greater than -2 but less than 4 lie in the interval
View SolutionAll the values of m for whilch both the roots of the equation x^2-2m x+m^2-1=0 are greater than -2 but less than 4 lie in the interval -2 3 c. -1
View Solutionfor what values of m, the equation 2x2−2(2m+1)x+m(m+1)=0,m∈R has
(i) Both roots smallar than 2 ?
(ii) Both roots greater than 2 ?
(iii) Both roots lie in the interval (2,3) ?
(iv) Exactly one root lie in the interval (2,3) ?
(v) One root is smaller than 1, and the other root is greater than 1 ?
(vi) One root is greater than 3 and the other root is smaller than 2 ?
(vii) Roots αandβ are such that both 2 and 3 lie between αandβ ?
View SolutionAll the values of m for whilch both the roots of the equation x^2-2m x+m^2-1=0 are greater than -2 but less than 4 lie in the interval
View SolutionAll the values of m for whilch both the roots of the equation x^2-2m x+m^2-1=0 are greater than -2 but less than 4 lie in the interval A -2 B. m >3 C. -1ltmlt3 D. 1ltmlt4
View Solution
