An examination was held on five subjects where the maximum marks for each subject was 100. X scored 82, 97, 88 and 91 marks in four subjects. If his total marks were 90% then, find his marks in the fifth subject.
पांच विषयों पर एक परीक्षा आयोजित की गई जहाँ प्रत्येक विषय के लिए अधिकतम अंक 100 थे | X ने 4 विषयों में क्रमश: 82, 97, 88 और 91 अंक प्राप्त किए | यदि उसके कुल अंक 90% थे, तो पांचवें विषय में उसने कितने अंक प्राप्त किए ?
92
89
94
79
The correct Answer is:A
Step by step video, text & image solution for An examination was held on five subjects where the maximum marks for each subject was 100. X scored 82, 97, 88 and 91 marks in four subjects. If his total marks were 90% then, find his marks in the fifth subject. पांच विषयों पर एक परीक्षा आयोजित की गई जहाँ प्रत्येक विषय के लिए अधिकतम अंक 100 थे | X ने 4 विषयों में क्रमश: 82, 97, 88 और 91 अंक प्राप्त किए | यदि उसके कुल अंक 90% थे, तो पांचवें विषय में उसने कितने अंक प्राप्त किए ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
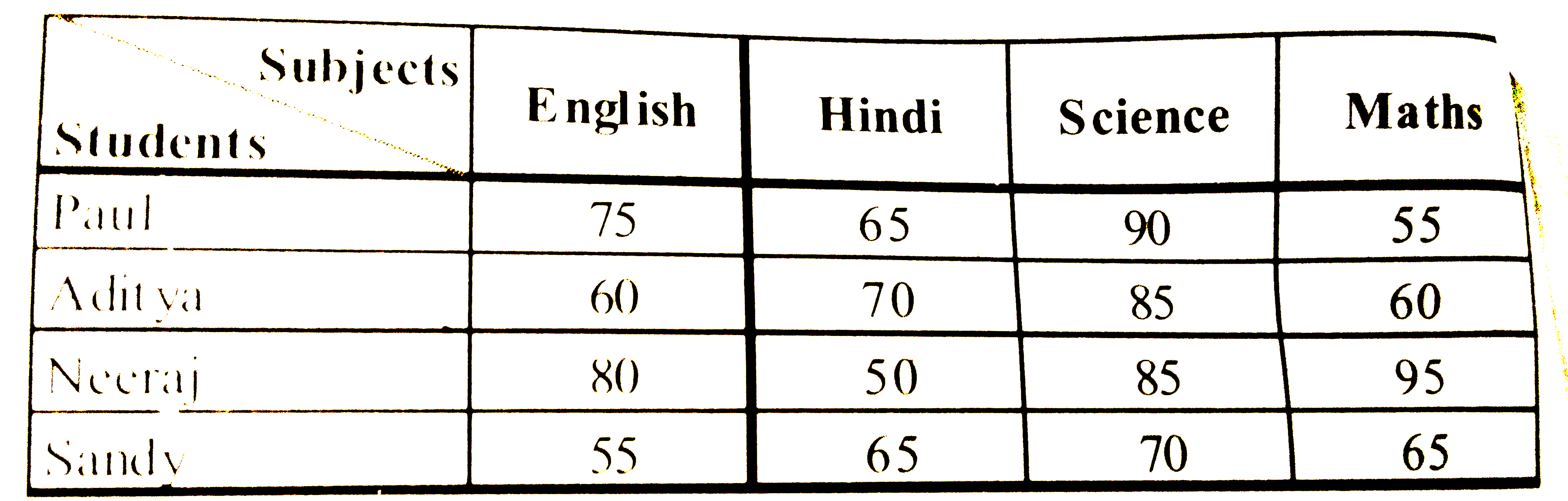
If maximum maks for each subject are 100 then find what percentage of total marks is obtained by sandy ?
View SolutionThe table given below shows the marks obtained by 4 students in 5 subjects. The maximum marks of each subject is 100.
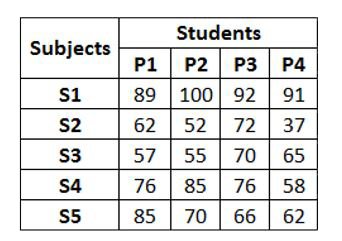
What are the average marks per subject obtained by P2?
View Solution
Knowledge Check
Highest marks are scored in the subject
AEnglishBHindiCMathsDNone of theseRavi had five subjects in his final examination. The maximum marks in each subject are 100. If his percentage in four subjects is 80, and he scores 65 marks in the fifth subject, determine his overall percentage for the five subjects.
A0.78B0.79C0.77D0.76A student got 430 marks in five subjects. How many marks did he get in English ?
(I) His average marks in other four subjects is 84.
(II) His marks in English is 8 more than his average marks in five subject.AIf statement I alone is sufficient but statement Il alone is not sufficient.BIf statement Il alone is sufficient but statement I alone is not sufficient.CIf each statement alone (either I or II) is sufficient.DIf statement I and II together are not sufficient.
A child scored 75 marks in each of five subjects. What is the median marks obtained by the child ?
View SolutionIn an examination there are three subjects of 100 marks each. A student scores 60% in the first subject and 80% in the second subject. He scored 70% in aggregate. His percentage of marks in the third subject is
View SolutionA student has to secure 35% marks to pass in a subject. If he gets 82 and fails by 23 marks. What is the maximum mark of the subject ?
View SolutionOf the 5 subjects, the average marks of Rakesh in first 3 Subjects was 79 and the average marks in the last 3 subjects was 86. If his marks in the third subject was 80, then what was his average marks in all the 5 subjects?
View SolutionAkhil scored 62, 70, 56, 85, 77, and 70 marks in six different subjects. The maximum mark in each subject is 100. Find his average score.
View Solution
