I is the incentre of ΔABCof∠A=46∘ , then ∠BIC = ?
93∘
113∘
124∘
134∘
The correct Answer is:B
To find the angle ∠BIC in triangle ABC where I is the incenter and ∠A=46∘, we can use the following steps:
1. Understand the Incenter:
The incenter I of a triangle is the point where the angle bisectors of the triangle intersect. It is equidistant from all sides of the triangle.
2. Use the Formula for ∠BIC:
The formula to find ∠BIC in terms of the angles of triangle ABC is:
∠BIC=90∘+∠A2
3. Substitute the Value of ∠A:
Given that ∠A=46∘, we can substitute this value into the formula:
∠BIC=90∘+46∘2
4. Calculate 46∘2:
46∘2=23∘
5. Add the Values:
Now, add 90∘ and 23∘:
∠BIC=90∘+23∘=113∘
6. Conclusion:
Therefore, the measure of ∠BIC is 113∘.
Final Answer:
∠BIC=113∘
The incenter I of a triangle is the point where the angle bisectors of the triangle intersect. It is equidistant from all sides of the triangle.
The formula to find ∠BIC in terms of the angles of triangle ABC is:
∠BIC=90∘+∠A2
Given that ∠A=46∘, we can substitute this value into the formula:
∠BIC=90∘+46∘2
46∘2=23∘
Now, add 90∘ and 23∘:
∠BIC=90∘+23∘=113∘
Therefore, the measure of ∠BIC is 113∘.
∠BIC=113∘
Similar Questions
Knowledge Check
P is the incentre of ΔABC. If ∠CAB=66∘,and∠CPY=46∘, find ∠PBA ?
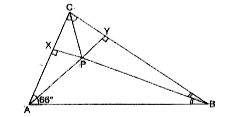 A16∘B23∘C13∘D18∘
A16∘B23∘C13∘D18∘If I is the incentre of △ABC and ∠A = 60∘, then the value of ∠BIC is
A100∘B120∘C150∘D110∘If O is the incentre of a triangle ABC and ∠AOC=124∘, find the ∠ABC.
A56B112C68Dcan't be determined
I is the incentre of ΔABC,∠ABC=60∘ and ∠ACB=50∘. Then find ∠BIC.
View SolutionS is the incentre of △PQR . If ∠PSR=125∘, then the measure of ∠PQR is:
View SolutionI is the incentre of the triangle ABC. If ∠ABC=60∘ and ∠ACB=50∘ then ∠BIC is
View SolutionI is the incentre of a triangle ABC. If ∠ABC=65∘ and ∠ACB=55∘, then the value of ∠BICis
View SolutionIf in a ΔABC,∠A=45∘,∠B=75∘, then
View Solution
