If angles M and N measure 60∘and30∘ respectively , (sin M) × (cot N) = ?
A. 1/2
B. √3/2
C. 3/2
D. 0
D
B
A
C
The correct Answer is:D
To solve the problem, we need to calculate sinM×cotN where M=60∘ and N=30∘.
1. Identify the values of sin and cot:
- We know that sin60∘=√32.
- We also need to find cot30∘.
2. Calculate cot30∘:
- Recall that cotθ=1tanθ.
- We know that tan30∘=1√3.
- Therefore, cot30∘=1tan30∘=√3.
3. Substitute the values into the expression:
- Now we substitute the values we found into the expression:
sinM×cotN=sin60∘×cot30∘=(√32)×√3
4. Perform the multiplication:
- Multiply the two fractions:
√32×√3=√3×√32=32
5. Final answer:
- Therefore, the value of sinM×cotN is 32.
Conclusion:
The answer is 32, which corresponds to option C.
---
- We know that sin60∘=√32.
- We also need to find cot30∘.
- Recall that cotθ=1tanθ.
- We know that tan30∘=1√3.
- Therefore, cot30∘=1tan30∘=√3.
- Now we substitute the values we found into the expression:
sinM×cotN=sin60∘×cot30∘=(√32)×√3
- Multiply the two fractions:
√32×√3=√3×√32=32
- Therefore, the value of sinM×cotN is 32.
The answer is 32, which corresponds to option C.
Similar Questions
As body of mass 5 kg is suspended by the stirngs making angles 60∘ and 30∘ with the horizontal :
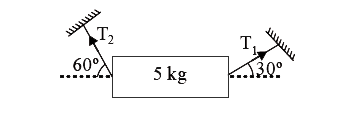
(a) T1=25N (b) T2=25N
( c ) T1=25√3N ( d ) T2=25√3N
View SolutionA body of mass 5kg is suspended by the strings making angles 60∘ and 30∘with the horizontal -
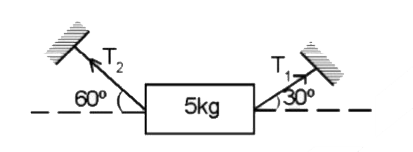
(a) T1=25N ( b) T2=25N
(c ) T1=25√3N (d) T2=25√3
View Solution
Knowledge Check
The value of sin60 is:
A. √1/2
B. √3/2
C. 1/√2
D. √1/√2ADBACCDBThe values of m, n respectively, if 108=2m×33×5n, are:
A2,0B3,1C0,1D2,2ΔDEF is right angled at E. If m∠F=60∘, then find the value of (cotD−2/√3).
A1−√2B1/√3C(2−√3)/2√3D(2−2√3)/√3.
IfA andBare two matrices of the order3×m and 3×n, respectively and m=n, then order of matrix (5A−2B) is (a) m×3 (b) 3×3 (c) m×n (d) 3×n
View SolutionIf the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 300 , 450 and 600 respectively, then the ratio, AB : BC, is : (1) √3:1 (2) √3:√2 (3) 1:√3 (4) 2:3
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
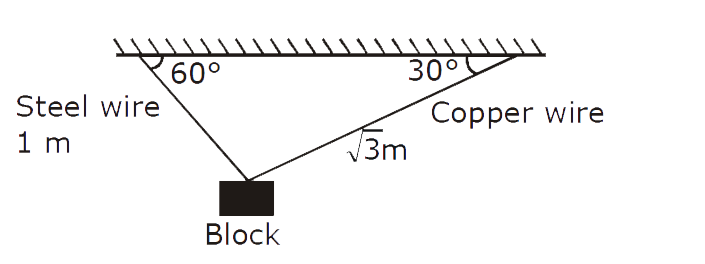
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionLet AD be a median of the ABC. If AEandAF are medians of the triangle ABDandADC , respectively, and AD=m1,AE=m2,AF=m3, thena28 is equal to (a)m22+m23−2m21 (b) m21+m22−2m23 (c)m21+m23−2m22 (d) none of these
View SolutionA body of mass 5 kg is suspended by the string making angles 60∘ and 30∘ with the horizontal
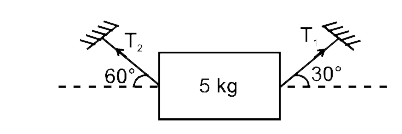
(a) T1=25N
(b) T2=25N
(c) T1=25√3N
(d) T2=25√3N
View Solution
