The sides of parallelogram are 12 m and 17 m respectively . If one of the diagonals is 25 m long the area of parallelogram is :
A)150m2
B)180m2
C)160m2
D)190m2
150m2
180m2
160m2
190m2
The correct Answer is:B
To find the area of the parallelogram with sides 12 m and 17 m, and one diagonal measuring 25 m, we can use Heron's formula to first calculate the area of one of the triangles formed by the diagonal.
1. Identify the sides of the triangle:
The triangle formed by the diagonal consists of the sides of the parallelogram and the diagonal. The sides are:
- Side A = 12 m
- Side B = 17 m
- Diagonal (Side C) = 25 m
2. Calculate the semi-perimeter (s):
The semi-perimeter s is calculated using the formula:
s=A+B+C2
Substituting the values:
s=12+17+252=542=27 m
3. Apply Heron's formula to find the area of triangle ABD:
Heron's formula for the area A of a triangle is given by:
A=√s(s−A)(s−B)(s−C)
Substituting the values:
A=√27×(27−12)×(27−17)×(27−25)
Simplifying:
A=√27×15×10×2
4. Calculate the area:
First, calculate the product inside the square root:
27×15=405
405×10=4050
4050×2=8100
Now, take the square root:
A=√8100=90 m2
5. Calculate the area of the parallelogram:
Since the diagonal divides the parallelogram into two equal triangles, the area of the parallelogram is:
Area of parallelogram=2×Area of triangle ABD=2×90=180 m2
Final Answer:
The area of the parallelogram is 180 m².
The triangle formed by the diagonal consists of the sides of the parallelogram and the diagonal. The sides are:
- Side A = 12 m
- Side B = 17 m
- Diagonal (Side C) = 25 m
The semi-perimeter s is calculated using the formula:
s=A+B+C2
Substituting the values:
s=12+17+252=542=27 m
Heron's formula for the area A of a triangle is given by:
A=√s(s−A)(s−B)(s−C)
Substituting the values:
A=√27×(27−12)×(27−17)×(27−25)
Simplifying:
A=√27×15×10×2
First, calculate the product inside the square root:
27×15=405
405×10=4050
4050×2=8100
Now, take the square root:
A=√8100=90 m2
Since the diagonal divides the parallelogram into two equal triangles, the area of the parallelogram is:
Area of parallelogram=2×Area of triangle ABD=2×90=180 m2
The area of the parallelogram is 180 m².
Similar Questions
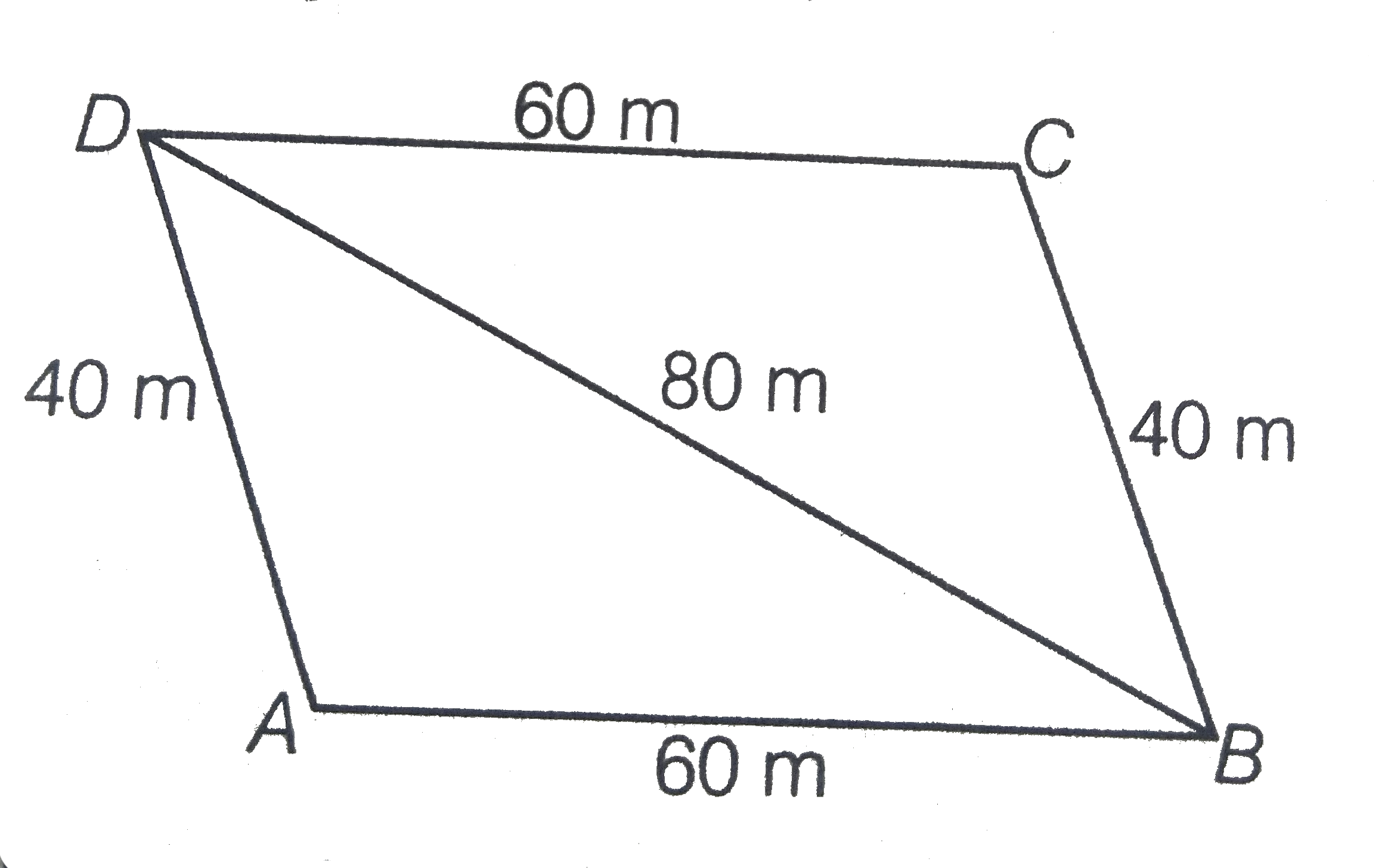
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionThe given figure shows a parallelogram of 20 m height. The base of the parallelogram is 40 m long.
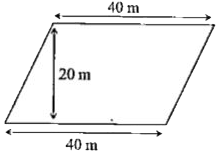
What is the area of the parallelogram?
View Solution
Knowledge Check
Diagonals of a parallelogram are 8 m and 6 m respectively. If one of side is 5m, then the area of parallelogram is:
A18m2B30m2C24m2D48m2Diagonals of a parallelogram are 8 m and 6 m respectively. If one of side is 5m, then the area of parallelogram is:
A18m2B30m2C24m2D48m2A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
 A480 sq. mB320 sq. mC600√15sq.mD450√15 sq . M
A480 sq. mB320 sq. mC600√15sq.mD450√15 sq . M
A rectangle and a parallelogram are drawn between the same parallel lines on a common base of 10 cm. If the perimeter of the rectangle is 36 cm, then the area of the parallelogram is 60cm2 (b) 80cm2 (c) 81cm2 (d) 100cm2
View SolutionOne side of a rectangular field is 15 m and one of its diagonals is 17 m. Find the area of the field.
View SolutionA parallelogram has sides 30m and 14m and one of its diagonals is 40 m long. Then, its area is 168 m2 (b) 336 m2 (c) 372 m2 (d) 480 m2
View SolutionA parallelogram has sides 30 m, 70 m and one of its diagonals is 80 m long. Its area will be
View SolutionA parallelogram has two sides 60 m and 25 m and a diagonal 65 m long. The area of the parallelogram is :
View Solution
