Which of the fractions given below is not equal to 59 ?
105198
80144
4072
2545
The correct Answer is:A
To determine which of the given fractions is not equal to 59, we will evaluate each option one by one.
Step 1: Evaluate the first fraction 105198
1. Simplifying 105198:
- Find the greatest common divisor (GCD) of 105 and 198.
- The GCD of 105 and 198 is 3.
- Now, divide both the numerator and the denominator by their GCD:
105÷3198÷3=3566
- Next, check if 3566 can be simplified further. The GCD of 35 and 66 is 1, so it cannot be simplified further.
2. Comparing with 59:
- Since 3566 cannot be simplified to 59, we can conclude that 105198 is not equal to 59.
Step 2: Evaluate the second fraction 80144
1. Simplifying 80144:
- Find the GCD of 80 and 144, which is 16.
- Divide both the numerator and the denominator by their GCD:
80÷16144÷16=59
- This fraction simplifies to 59.
Step 3: Evaluate the third fraction 4072
1. Simplifying 4072:
- Find the GCD of 40 and 72, which is 8.
- Divide both the numerator and the denominator by their GCD:
40÷872÷8=59
- This fraction also simplifies to 59.
Step 4: Evaluate the fourth fraction 2545
1. Simplifying 2545:
- Find the GCD of 25 and 45, which is 5.
- Divide both the numerator and the denominator by their GCD:
25÷545÷5=59
- This fraction simplifies to 59.
Conclusion
After evaluating all the fractions, we find that the only fraction that does not equal 59 is 105198.
Thus, the answer is:
The fraction that is not equal to 59 is 105198.
---
- Find the greatest common divisor (GCD) of 105 and 198.
- The GCD of 105 and 198 is 3.
- Now, divide both the numerator and the denominator by their GCD:
105÷3198÷3=3566
- Next, check if 3566 can be simplified further. The GCD of 35 and 66 is 1, so it cannot be simplified further.
- Since 3566 cannot be simplified to 59, we can conclude that 105198 is not equal to 59.
- Find the GCD of 80 and 144, which is 16.
- Divide both the numerator and the denominator by their GCD:
80÷16144÷16=59
- This fraction simplifies to 59.
- Find the GCD of 40 and 72, which is 8.
- Divide both the numerator and the denominator by their GCD:
40÷872÷8=59
- This fraction also simplifies to 59.
- Find the GCD of 25 and 45, which is 5.
- Divide both the numerator and the denominator by their GCD:
25÷545÷5=59
- This fraction simplifies to 59.
The fraction that is not equal to 59 is 105198.
Similar Questions
Knowledge Check
Which of the fractions given below is not equal to 411
A3288B84209C64176D2055Which of the fractions given below is not equal to 411?
A3288B84209C64176D2055Which of the fractions given below, when added to 135, gives 1 ?
A−815B−75C−2610D−4830
Which of the fractions given below, when added to 57 gives 1?
View SolutionThe fraction which is not equal to is
View SolutionIs 59 equal to 45 ?
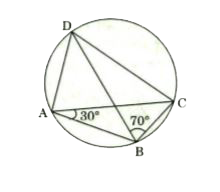
View SolutionIn the figure given below, what is ∠BCD equal to ?
View SolutionFrom the fractions given below separate proper fractions 517,117,38,97,1114,76,58,315,259,1310,1817,1819,2137,1516
View Solution
