An inductor (L=20mH), a resistor (R=100Ω) and a battery(ɛ=10V) are connected in series. Find (a) the time constant, (b) the maximum current and (c ) the time elapsed before the current reaches 99% of the maximum value. Solution in Tamil
(a) The time constant is τ=LR=20mH100Ω=0<br>20ms<br>(b)Themaxiμmcurrentis I = varepsilon /R = (10 V)/(100 Omega) = 0
10 A<br>(c)UsingI = i_0(1-e^(-t/tau), 0
99 i_0 = i_0(1-e^(-t/tau)or, e^(-t/tau) = 0
01)or,(t)/(tau) =- In(0
01)or,t = (0
20ms) In(100) = 0
92ms.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Worked out examples
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
9 Videos
Similar Questions
A conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View SolutionA short magnet is moved along the axis of a conducting loop. Show that the loop repels the magnet if the magnet is approaching the loop and attracts the magnet if it is going away from the loop.
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (verepsilon = 10 V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the cirucit 1ms after short- circuititig.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before (a) the current reaches half its maximum value, (b) the power dissipated in heat reaches half its maximum value and © the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA solenoid having inductance 4.0 H and resistance 10 Omega is connected to a 4.0 V battery at t = 0. Find (a) the time constant, (b) the time elapsed before the current reached 0.63 of its steady state value, (c ) the power delivered by the battery at this instant and (d) the power dissipated in Joule heating at this instant.
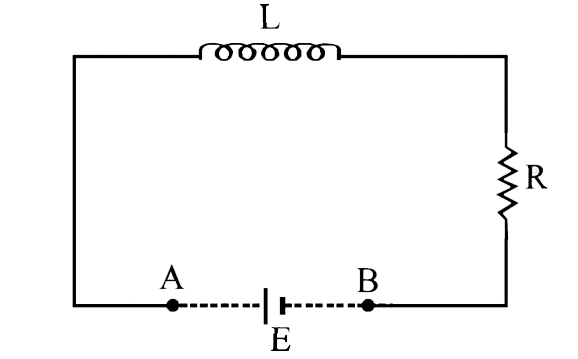
View SolutionAn inductor (L=100mH), a resistor (R=100(Ω)) and a battery (E=100V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the point A and B. The current in the circuit 1 ms after the short circuit is
View SolutionA 1 -k Omega resistor is connected in series with a 10-mH inductor, a 30 V battery and an open switch. At time t= 0 , the switch is suddenly closed. a. What is the maximum current in this circuit and when does it occur? b. What are the voltage drops across the inductor and across the resistor 20 mu s after the switch is closed? c. On a single set of axes, sketch the voltage across the resistor and the voltage across the inductor as functions of time. Also, sketch a graph of the current in the circuit as s function of time.
View SolutionA 20 mH coil is connected in series with a 2kΩ resistor and a 12 V battery.
Calcualte
(i) time constant of the circuit,
(ii) time during which current decrys to 10% of its maximum value.
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Omega . Calculate the time constant. What will be the maximum value of current in the circuit ?
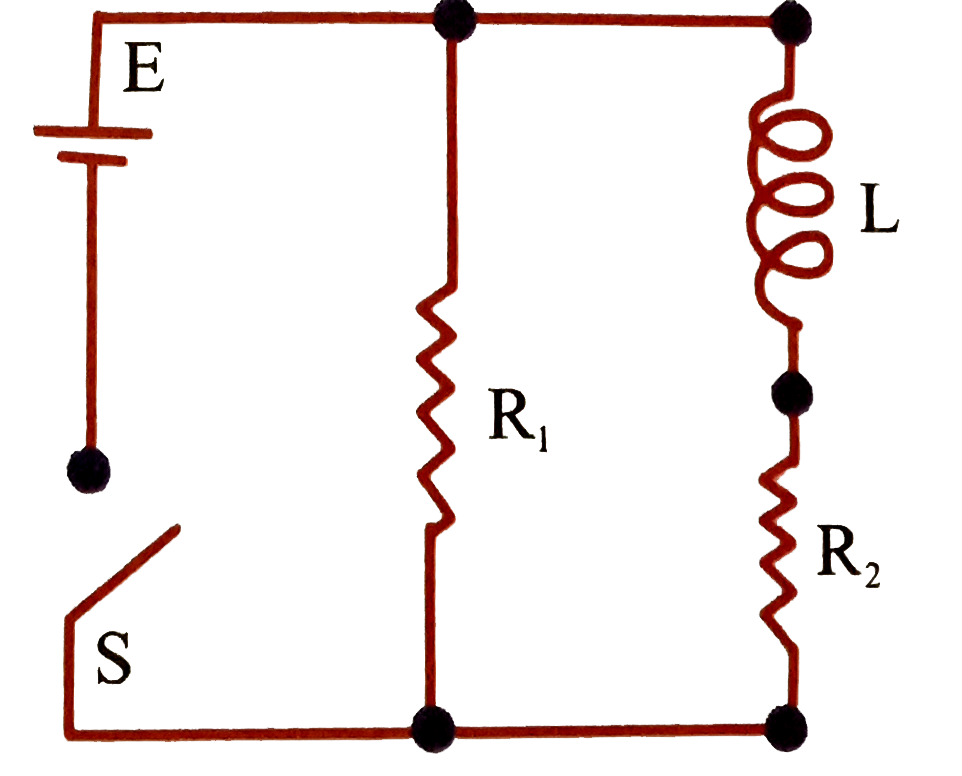
View SolutionAn inductor (L=100mH), a resistor (R=100Ω), and a battery (W=100V) are initially connected in series as shown by the figure. After a long time the battery is disconnected after short circuiting the points A and B. The currents in the circuit 1mm after the short circuit is
View SolutionA 100 V battery, a 5.00 V resistor, and a 10.0 H inductor are connected in series. After the current in th circuit has reached its maximum value.
View SolutionAn L-R combination is connected to an ideal battery. If L=20mH,R=100Ω and ε=10V, find (i) the time constant (ii) the maximum current and (iii) the time elapsed before the current reaches 90% of the maximum value.
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (ε=10V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the circuit 1ms after short- circuiting.
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Omega . Calculate the time constant. What will be the maximum value of current in the circuit ?
View Solution
