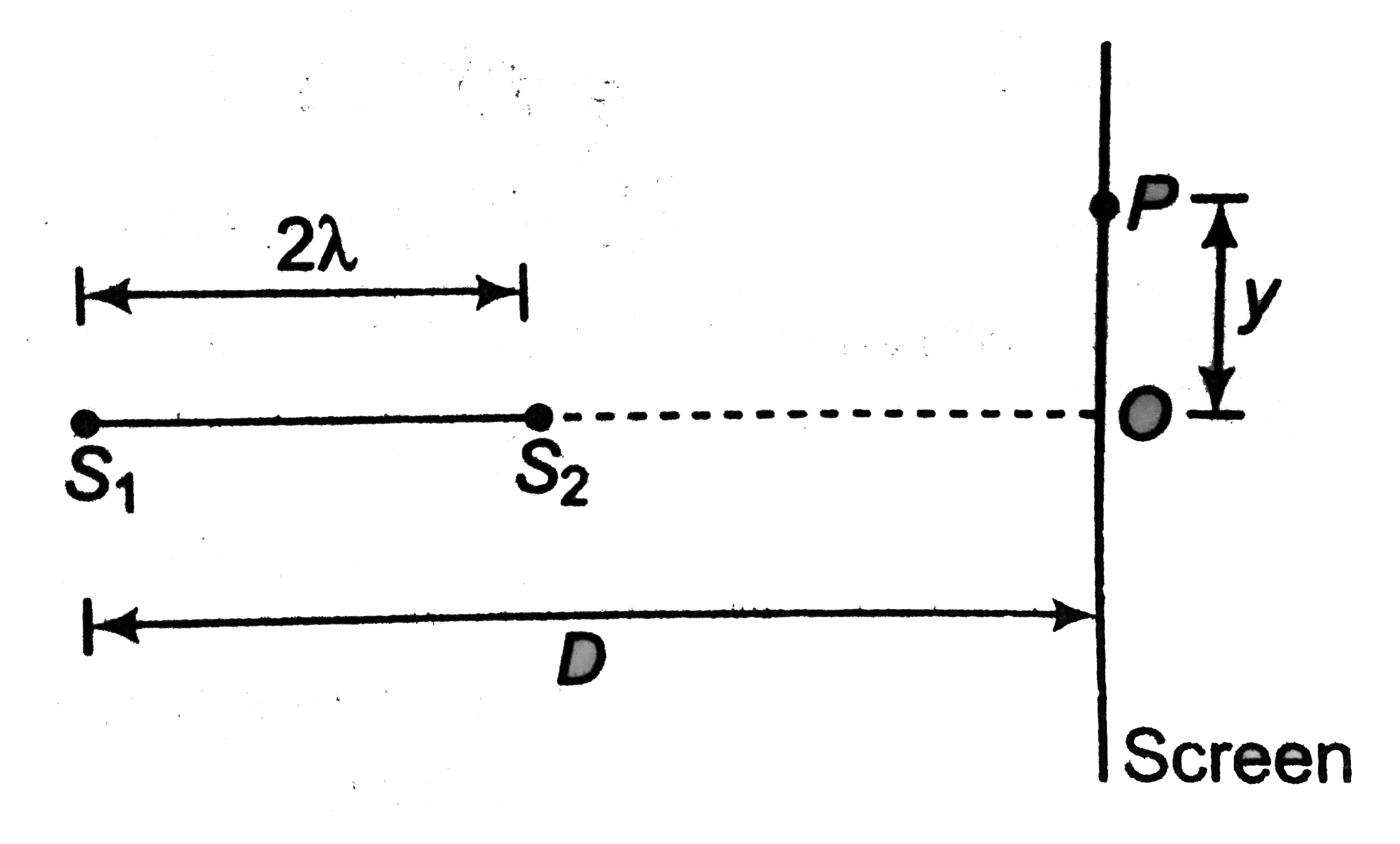
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallet to each other at a small separation of 2λ . The sound is delected by maving a delector on the screen at a distance D(>>λ) from the slit S1 as shows in figure. Find the distance y such that the intensity at P is equal to intensity at O .
 Solution in Tamil
Solution in Tamil
The correct Answer is:C, D
Since S1,S2 are in same phase at O there wil be maximum intensity.
Given that there will be a maximum intensity at P.
→pathd⇔erence=△x=nl

From the ure (in question)
(S1P)2−(S2P)2
=(sqrtD^2+x_2)^2-[(sqrtD-2lamda^2+x^2]^2<br>=4lamdaD=4lamda^2=4lamdaD<br>(lamda^2issosmallandcan²cted)<br>S_1P-S_2P=(4lamdaD)/(2sqrt(x^2+D^2))=nlamda<br>=(2D)/(sqrt(x^2+D^2))=n<br>rarr n^2(x^2+D^2)=4D^2<br>rarr x=D/n sqrt4-n^2<br>Whenn=1, x=sqrt3D(1st order)<br>n=2,<br>x=0 (2nd order)
∴Wenx=√3D
at P there will be maximum intensity
Topper's Solved these Questions
Similar Questions
A load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View Solution0.32g of oxygen is kept in a rigid container and is heated. Find the amount of heat needed to raise the temperature from 250C→350C. The molar heat capacity of oxygen at constant volume is 20JK−1mol−1.
View SolutionTwo coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2lamda . The sound is detected by moving a detector on the screen sum at a distance D(gtgtlamda) from the slit S_1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
View SolutionTwo coherent narrow slits emitting wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda , the sound is detected by moving a detector on the screen S at a distance D (gtgt lambda) from the slit S_(1) as shown in Fig. 7.76. Find the distance x such that the intensity at P is equal to the intensity at O .
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
View SolutionTwo coherent narrow slits emitting light of wavelength lamda in the same phase are placed parallel to each other at a small separation of 3lamda the light is collected on a screen S which is placed at a distance D(gt gt lamda) from the slits the smallest distance x such that the P is a maxima.
View SolutionTwo coherent point sources S_1 and S_2 vibrating in phase emit light of wavelength lamda . The separation between them is 2lamda . The light is collected on a screen placed at a distance Dgt gt lamda from the slit S_1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......
View SolutionTwo coherant narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda .The light is collected on a screen S which is placed at a distance D( gt gt A) from the slit S_(1) as shown in figure .Find teh finite distance x such that the intensity of P is equal to intensity at O .
View SolutionTwo coherent narrow slits emitting light of wavelength lambda in the same phase are placed parallel to each other at a small separation of 2lambda . The light is collected on a screen S which is placed at a distance D(gtgt lambda ) from the slit S_1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O. .
View SolutionThe intensity at the maximum in a Young's double slit experiment is I_(0) . Distance between two slits is d=5 lambda , where lambda is the wavelength of light used in the experiment. The intensity infront of one of the slits on the screen placed at a distance D=10 d is (I_(0))/(n) . Find n .
View Solution_S01_032_Q01.png)
Figure shows two coherent microwave source S1 and S2 emitting waves of wavelength λ and separated by a distance 3λ for λ<<D and y≠0. The minimum value of y for point P to be an intensity maximum is √mDn determine the value of m+n, if m and n are coprime numbers.
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
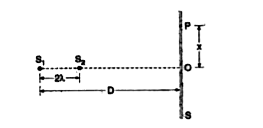
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(>>λ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity at O.
View Solution
