When an integer n is divided by 7, the remainder is 3. What will be the remainder if 6n is divided by 7 ?
2
4
1
0
The correct Answer is:B
To solve the problem, we start with the information given:
1. When an integer n is divided by 7, the remainder is 3. This can be expressed mathematically as:
n=7k+3
where k is some integer.
2. We need to find the remainder when 6n is divided by 7. First, we calculate 6n:
6n=6(7k+3)=42k+18
3. Now, we need to find the remainder of 42k+18 when divided by 7. We can simplify this by finding the remainders of each term:
- The term 42k is divisible by 7, so:
42kmod7=0
- Next, we find the remainder of 18 when divided by 7:
18÷7=2(since 7×2=14)
The remainder is:
18−14=4
4. Therefore, when we combine these results, we have:
6nmod7=(42k+18)mod7=(0+4)mod7=4
Thus, the remainder when 6n is divided by 7 is 4.
n=7k+3
where k is some integer.
6n=6(7k+3)=42k+18
- The term 42k is divisible by 7, so:
42kmod7=0
- Next, we find the remainder of 18 when divided by 7:
18÷7=2(since 7×2=14)
The remainder is:
18−14=4
6nmod7=(42k+18)mod7=(0+4)mod7=4
Similar Questions
Knowledge Check
If a positive integer 'n' is divided by 7, the remainder is 4. What is the remainder if 5n' is divided by 7?
AA)6BB)5CC)3DD)4When N is divided by 4, the remainder is 3. What is the remainder when 2N is divided by 4.
A2B3C4D8When N is divided by 10 the remainder is 8. What is the remainder when N is divided by 5.
A3B2C1D4
When n is divided by 4, the remainder is 3. What is the remainder when 2n is divided by 4? 1 (b) 2 (c) 3 (d) 6
View SolutionIf 5 divided the integer n, the remainder is 2. What will be the remainder if 7n is divided by 5?
यदि 5 से पूर्णाक n में भाग दिया जाए, तो शेषफल 2 आता है | यदि 7n में 5 से भाग दिया जाए, तो शेषफल कितना आएगा ?
View SolutionIf 5 divides the integer n, the remainder is 2. What will be the remainder if 7n is divided by 5 ?
View SolutionWhen 'n' is divisible by 5 the remainder is 2. What is the remainder when n2 is divided by 5 ?
View SolutionWhen n is divided by 4, the remainder is 3. The remainder when 2n is divided by 4 is :
View Solution

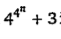 is divided by 7 is:
is divided by 7 is: