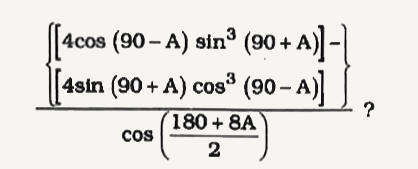
What is value of [11−x(p−q)+11−x(q−p)]?
0
1
(xq−xp/(xq+xp)
(xq+xp)/(xq−xp)
The correct Answer is:A
To solve the expression (11−x(p−q)+11−x(q−p)), we will follow these steps:
Step 1: Rewrite the Expression
We start with the given expression:
11−x(p−q)+11−x(q−p)
Step 2: Identify the Terms
Notice that x(q−p) can be rewritten as 1x(p−q). Thus, we can rewrite the second term:
11−x(q−p)=11−1x(p−q)
Step 3: Simplify the Second Term
To simplify 11−1x(p−q), we can find a common denominator:
1−1x(p−q)=x(p−q)−1x(p−q)
Thus, the second term becomes:
x(p−q)x(p−q)−1
Step 4: Combine the Two Terms
Now we have:
11−x(p−q)+x(p−q)x(p−q)−1
We can find a common denominator for these two fractions:
(1−x(p−q))(x(p−q)−1)
Step 5: Write the Combined Fraction
The combined fraction becomes:
(x(p−q)−1)+(1−x(p−q))(1−x(p−q))(x(p−q)−1)
The numerator simplifies to:
x(p−q)−1+1−x(p−q)=0
Step 6: Conclusion
Since the numerator is zero, the entire expression evaluates to zero:
0(1−x(p−q))(x(p−q)−1)=0
Thus, the value of the expression is:
0
We start with the given expression:
11−x(p−q)+11−x(q−p)
Notice that x(q−p) can be rewritten as 1x(p−q). Thus, we can rewrite the second term:
11−x(q−p)=11−1x(p−q)
To simplify 11−1x(p−q), we can find a common denominator:
1−1x(p−q)=x(p−q)−1x(p−q)
Thus, the second term becomes:
x(p−q)x(p−q)−1
Now we have:
11−x(p−q)+x(p−q)x(p−q)−1
We can find a common denominator for these two fractions:
(1−x(p−q))(x(p−q)−1)
The combined fraction becomes:
(x(p−q)−1)+(1−x(p−q))(1−x(p−q))(x(p−q)−1)
The numerator simplifies to:
x(p−q)−1+1−x(p−q)=0
Since the numerator is zero, the entire expression evaluates to zero:
0(1−x(p−q))(x(p−q)−1)=0
0
Similar Questions
Knowledge Check
What is the value of I1
A2πBπCπ/2D2π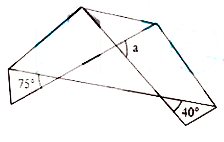
What is the value of a?A65∘B75∘C105∘D115∘What is the value of B?
A815B1615C3215D0