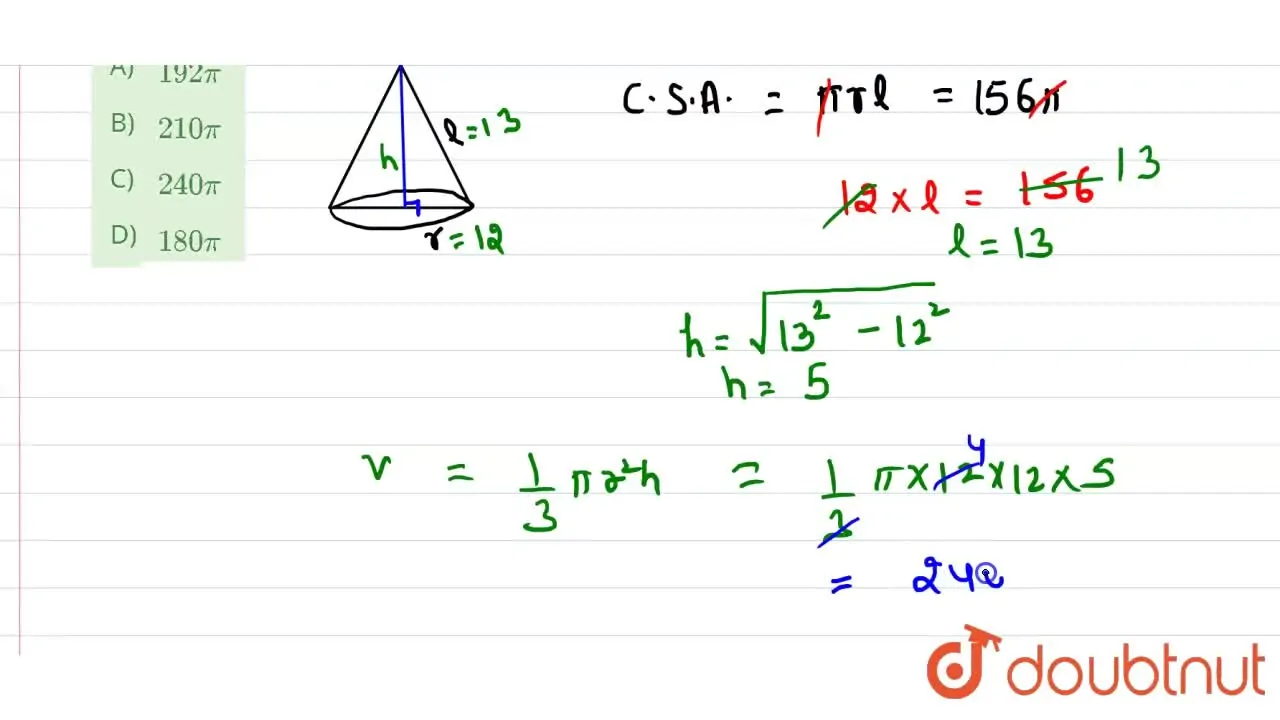
The curved surface area of a right circular cone is 156π and the radius of its base is 12 cm. What is the volume of the cone, in cm3 ?
192π
210π
240π
180π
The correct Answer is:C
Step by step video, text & image solution for The curved surface area of a right circular cone is 156pi and the radius of its base is 12 cm. What is the volume of the cone, in "cm"^(3) ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
The curved surface area of a right circular cone is 1.76m2 and its base diameter is 140 cm. What is the height of the cone ?
View SolutionThe curved surface area of a cone is 550cm sq . If the area of its base is 154 cm sq , then what will be the volume of the cone?
View SolutionThe vertical height of a right circular cone is 9 cm and radius of its base is 4 cm. Find its volume.
View SolutionFind the curved surface area of a cone, if its slant height is 60cm and the radius of its base is 21cm.
View SolutionThe height of a right circular cone is 6 cm and area of its base is 18.5cm2. Find its volume.
View SolutionThe curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is ……………. .
View SolutionThe curved surface area of a right circular cone of radius 14 cm is 440 sq cm. What is the slant height of the cone?
View SolutionThe volume of a right circular cone is 1232 cm^3. If the radius of its base is 14 cm, find its curved surface.
View SolutionFind the curved surface area of a right circular cone whose slant height is 10cm and base radius is 7cm.
View SolutionFind the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm
View Solution