A field is in the shape of a trapezium whoseparallel sides are 200 m and 400 m long, whereas each of other two sides is 260 m long. What is the area (in )of the field?
78000
52000
72000
60000
The correct Answer is:C
To find the area of the trapezium-shaped field, we can follow these steps:
Step 1: Identify the trapezium dimensions
We know the lengths of the parallel sides:
- AB (top parallel side) = 200 m
- CD (bottom parallel side) = 400 m
- The lengths of the non-parallel sides (AD and BC) = 260 m each.
Step 2: Draw the trapezium
Draw trapezium ABCD with AB and CD as the parallel sides. Label the sides accordingly:
- AB = 200 m
- CD = 400 m
- AD = BC = 260 m
Step 3: Drop perpendiculars
Drop perpendiculars from points A and B to line CD. Let these perpendiculars meet CD at points E and F respectively. Thus, AE and BF are the heights of the trapezium.
Step 4: Calculate the length of DE and FC
Since AB is parallel to CD, we can find the lengths DE and FC:
- DE + EF + FC = CD
- EF = AB = 200 m
- Therefore, DE + FC = 400 m - 200 m = 200 m.
Since DE = FC (because of symmetry), we can set DE = FC = x:
- 2x = 200 m
- x = 100 m.
Thus, DE = 100 m and FC = 100 m.
Step 5: Use the Pythagorean theorem
Now, we can use the Pythagorean theorem in triangle AED (or triangle BFC):
- AD² = AE² + DE²
- 260² = AE² + 100²
- 67600 = AE² + 10000
- AE² = 67600 - 10000
- AE² = 57600
- AE = √57600
- AE = 240 m.
Step 6: Calculate the area of the trapezium
Now that we have the height (AE = 240 m), we can use the formula for the area of a trapezium:
Area=12×(AB+CD)×height
Substituting the values:
Area=12×(200+400)×240
=12×600×240
=300×240
=72000m2.
Final Answer
The area of the field is 72000 m².
---
We know the lengths of the parallel sides:
- AB (top parallel side) = 200 m
- CD (bottom parallel side) = 400 m
- The lengths of the non-parallel sides (AD and BC) = 260 m each.
Draw trapezium ABCD with AB and CD as the parallel sides. Label the sides accordingly:
- AB = 200 m
- CD = 400 m
- AD = BC = 260 m
Drop perpendiculars from points A and B to line CD. Let these perpendiculars meet CD at points E and F respectively. Thus, AE and BF are the heights of the trapezium.
Since AB is parallel to CD, we can find the lengths DE and FC:
- DE + EF + FC = CD
- EF = AB = 200 m
- Therefore, DE + FC = 400 m - 200 m = 200 m.
- 2x = 200 m
- x = 100 m.
Now, we can use the Pythagorean theorem in triangle AED (or triangle BFC):
- AD² = AE² + DE²
- 260² = AE² + 100²
- 67600 = AE² + 10000
- AE² = 67600 - 10000
- AE² = 57600
- AE = √57600
- AE = 240 m.
Now that we have the height (AE = 240 m), we can use the formula for the area of a trapezium:
Area=12×(AB+CD)×height
Substituting the values:
Area=12×(200+400)×240
=12×600×240
=300×240
=72000m2.
The area of the field is 72000 m².
Similar Questions
A plot is in the shape of a trapezium. The parallel sides of the plot are 20 m and 16 m long, and the distance between them is 8 m. A square plot has the same area as the trapezium. A pit of dimensions 2.4 m long, 1.5 m wide, and 1 m deep is dug inside the trapezium plot and the soil is spread uniformly on the square plot. Find the rise in the level of hte plot.
View SolutionA plot is in the shape of a trapezium. The parallel sides of the plot are 20 m and 16 m long, and the distance between them is 8 m. A square plot has the same area as the trapezium. A pit of dimensions 2.4 m long, 1.5 m wide, and 1 m deep is dug inside the trapezium plot and the soil is spread uniformly on the square plot. Find the rise in the level of hte plot.
View Solution
Knowledge Check
The parallel sides of trapezium field are 12 m and 20 m . If distnace between the parallel sides is 8 m, find the area of the field
A128 sq mB132 sq mC130 sq mD135 sq mThe parallel sides of a trapezium field are 12 m and 20 m. If distance between the parallel sides is 8 m, find the area of the field.
A128 sqmB132 sq mC130 sq mD135 sq mThe length of two parallel sides of a trapezium are 18 m and 24 m. If its height is 12 m, what is the area (in m2) of the trapezium ?
A126B252C504D1024
A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the thired side at right angles. The length of the fourth side is 100 m. If it costs Rs. 5 to plough 1 m2 of the field, find the total cost of ploughing the field.
View SolutionA field is in the shape of a trapezium having parallel sides 90m and 30m.
These sides meet the third side at right angles. The length of the fourth side is 100m. If it costs rupee 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
View SolutionFind the area of a triangular field whose sides are 78 m, 50 m and 112 m.
View SolutionFind the area of trapezium having length of parallel sides 25 m and 15 m .The distance between the parallel sides is 8 m.
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
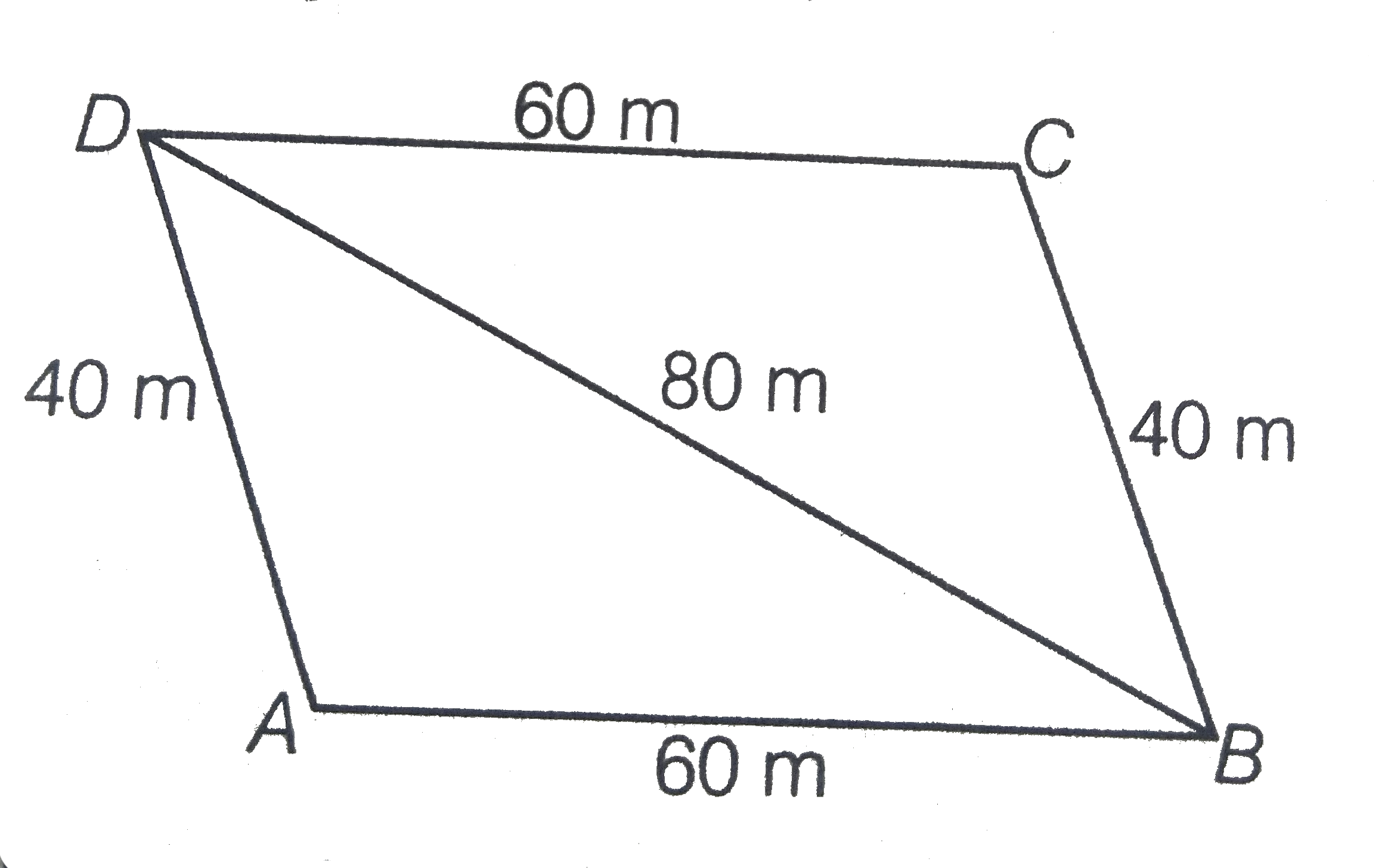
View Solution