सोडियम प्रकाश के लिए, λ1 और λ2 तरंगदैर्यों पर दो पीली रेखाएं प्राप्त होती हैं। यदि इन दोनों का माध्य 6000Å और |λ2−λ1|=6Å है, तब λ1 और λ2 के संगत दो स्तरों के मध्य ऊर्जा अंतर लगभग है:
2×10−3eV
2eV
2000 eV
2×10−6 eV
The correct Answer is:A
दिया है,
λ1 और λ2 का माध्य =6000Å
|λ2−λ1|=6Å
अर्थात λ1+λ22=6000Å
λ1+λ2=12000Å .......(i)
λ2−λ1=6Å ......(ii)
समीकरण (i) और (ii) को बराबर करने पर, हमें प्राप्त होता है
2λ1=12006
λ2=120062=6003Å
और λ1=5997Å
अब, ऊर्जा अंतर
ΔE=hcλ1=hcλ2
ΔE=hc(1λ1−1λ2)
ΔE=6.6×10−34×3×108×(λ2−λ1λ1λ2)
=6.6×10−34×3×108×6×10−105997×10−10×6003×10−10×1.6×10−19eV
=2.12×10−3eV~−2×10−3eV
Topper's Solved these Questions
Similar Questions
v चाल से गतिमान एक H- परमाणु विराम अवस्था में एक अन्य H - परमाणु के साथ सम्मुख प्रत्यक्ष संघट्ट करता है। दोनों परमाणु मूल अवस्था में हैं। वेग v का न्यूनतम मान जिसके लिए कम से कम एक परमाणु उत्तेजित हो सकता है, है
View Solutionनिकाय का प्रारंभिक विन्यास चित्र में दिखाया गया है।
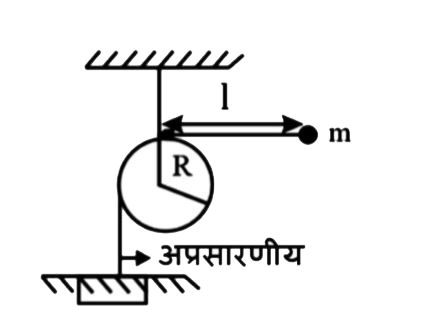
डोरी और घिरनी हल्की हैं। गोलक को मुक्त किया जाता है और डोरी घिरनी के चारों ओर लिपटना शुरू कर देती है। (घिरनी केंद्र पर अनुप्रयुक्त बल द्वारा स्थान पर रखी जाती है)
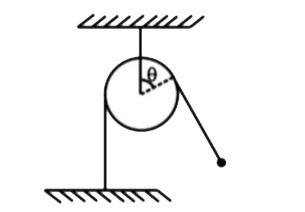
वह दर r ज्ञात कीजिए जिससे घिरनी के चारों ओर लपेटी गई डोरी की लंबाई बढ़ती ( θ के फलन के रूप में) है।
View SolutionIf a1=a,a2=b,an+2=an+1+an2,n≥0 then limn→∞an is a+λ1bλ2,(λ1,λ2εI) where λ1+λ2 is _______
View SolutionThe matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent if λ21+λ22+λ23=k where λ1,λ2,λ3 are non-zero real numbers. Then the value of (10+k)2 is . . .
View SolutionIf α,β are the roots fo the equation λ(x2−x)+x+5=0. If λ1 and λ2 are two values of λ for which the roots α,β are related by αβ+βα=45 find the value of λ1λ2+λ2λ1
View SolutionIf λ1andλ2 are the wavelengths of the first members of the Lyman and Paschen series respectively, then λ1:λ2 is
View SolutionFor Balmer series, wavelength of first line is lamda_(1) and for Brackett series, wavelength of first line is lamda_(2) then (lamda_(1))/(lamda_(2))
View SolutionIf |ai|<1λi≥0 for i=1,2,3,.......nandλ1+λ2+.......+λn=1 then the value of |λ1a1+λ2a2+.......+λnan| is :
View SolutionIf λ1 and λ2 are the two valyes of λ such that the α and β of quadratic equation λ(x2−x)+x−5=0 satisfy αβ+βα+45=0 then λ1λ22+λ2λ21 is equal to
View SolutionIf |a_(k)|lt1,lamda_(k)ge0 , Where k=1,2, . . ,n And lamda_(1)+lamda_(2)+ . . +lamda_n=1 , Then |lamda_(1)a_(1)+lamda_(2)a_(2)+ . . .+lamda_(n)a_(n)| The value of
View SolutionIf α,β are the roots of the equation λ(x2−x)+x+5=0 and if λ1andλ2 are two values of λ obtained from αβ+βα=4, then λ1λ22+λ2λ21 equals.
View SolutionIf α,β are the roots fo the equation λ(x2−x)+x+5=0. If λ1 and λ2 are two values of λ for which the roots α,β are related by αβ+βα=45 find the value of λ1λ2+λ2λ1
View SolutionThe matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent if λ21+λ22+λ23=k where λ1,λ2,λ3 are non-zero real numbers. Then the value of (10+k)2 is . . .
View SolutionIf |ai|<1λi≥0 for i=1,2,3,.......nandλ1+λ2+.......+λn=1 then the value of |λ1a1+λ2a2+.......+λnan| is :
View SolutionIn the transitions A, B and C (as shown) lamda_(1) = ( lamda_(2) lamda _(3))/(lamda_(2) - lamda _(3)) the wavelength lamda_(1) corresponds to which transition, if lamda _(2) and lamda_(1) corresponds to other two transitions
View SolutionIf a1=a,a2=b,an+2=an+1+an2,n≥0 then limn→∞an is a+λ1bλ2,(λ1,λ2εI) where λ1+λ2 is _______
View Solution
