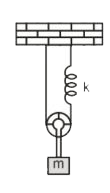
चित्र में दिखाए गए एक निकाय में एक द्रव्यमान रहित घिरनी, बल नियतांक k की एक स्प्रिंग और द्रव्यमान m का एक गुटका है। यदि गुटके को अपनी साम्यावस्था की स्थिति से ऊर्ध्वाधर नीचे की ओर हल्का सा विस्थापित किया जाता है और छोड़ दिया जाता है, तो ऊर्ध्वाधर दोलनों का आवर्त काल है:
The correct Answer is:B
इस स्थिति में, यदि द्रव्यमान m साम्यावस्था की स्थिति से x दूरी नीचे की ओर बढ़ता है, तब घिरनी भी x द्वारा आगे बढ़ेगी और इसलिए, स्प्रिंग 2x द्वारा फैल जाएगी।
इसलिए, स्प्रिंग बल 2kx होगा।
गुटके पर प्रत्यानयन बल 4k होगा।
अतः F=-4 kx
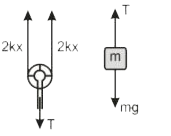
mg-4kx=ma
ma=-4kx + mg
Topper's Solved these Questions
Similar Questions
जब एक इलेक्ट्रॉन उच्च ऊर्जा अवस्था से ΔE इलेक्ट्रॉन - वोल्ट के ऊर्जा अंतर के साथ निम्न ऊर्जा अवस्था में जाता है, तो उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्ध्य लगभग होती है:
View Solutionएक परमाणु में एक इलेक्ट्रॉन के दो ऊर्जा स्तर 2. 3 eV द्वारा पृथक होते हैं। इलेक्ट्रॉनों के उच्च स्तर से निम्न स्तर पर जाने पर उत्सर्जित विकिरण की आवृत्ति है:
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View SolutionAn umbrella is marked for ₹ 150 and sold for ₹ 138. The rate of discount is:
एक छतरी का मूल्य ₹150 अंकित किया गया है और इसे ₹138 में बेचा जाता है। छूट की दर है:
View Solutionएक बंद पात्र में 25^(@)C पर साम्यावस्था SO_(2)CI_(2)(g) को प्राप्त किया जाता है और एक अक्रिय गैस, हीलियम को प्रवेशित किया जाता है । निम्नलिखित में से कौन सा कथन सही है ?
View Solutionएक प्रबल अम्ल की उपस्थिति में एक ऑक्सीम के एक एमाइड में पुनर्विन्यास को कहा जाता है:
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View SolutionH_(2) और I_(2) की समतुल्य मात्रा को एक संवृत पात्र में साम्यावस्था प्राप्त होने तक गर्म किया जाता है। यदि हाइड्रोजन का 80% , HI में परिवर्तित किया जा सकता है, तो इस ताप पर K_c है-
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionएक साइक्लोहेक्सेनोन, अम्ल उत्प्रेरक मात्रा की उपस्थिति में डाइमेथिलएमीन के साथ अभिक्रिया पर एक यौगिक का निर्माण करता है, यदि अभिक्रिया के दौरान जल का लगातार निष्कासन किया जाता है, तब निर्मित यौगिक को सामान्यतः जाना जाता है
View Solutionएक संकुल में केंद्रीय धातु परमाणु की उपसहसंयोजन संख्या को किसके द्वारा प्रदर्शित किया जाता है?
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solutionएक बंद ऊष्मारोधी पात्र में एक द्रव को इसके तापमान को बढ़ाने के लिए एक छड़ की सहायता से विडोलित किया जाता है। इस प्रक्रम में निम्नलिखित में से कौन सा सही है?
View Solutionएक AB ठोस में CSCI प्रकार की संरचना होती है, जहाँ A कोने पर स्थित होता है। यदि किसी एक काय विकर्ण के अनुदिश कोनों से परमाणुओं को हटा दिया जाता है, तो ठोस का सूत्र होगा ?
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@)=0.4 और P_(B)^(@)=1.2" atm" है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solution

