Question

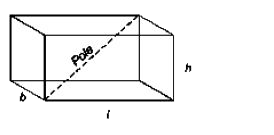
What is the length (in meters) of largest rod that can be placed in a room 8 m long, 5 m broad and 6 m high?

Options

A. 5
B. 10
C. `5sqrt5`
D. 12

Answer

C

Explanation

To find the length of the largest rod that can be placed in a room with dimensions 8 m long, 5 m broad, and 6 m high, we will calculate the diagonal of the cuboid formed by the room. The diagonal of a cuboid can be found using the formula:

$$d=\sqrt{l^2+b^2+h^2}$$

where:
- $$l$$ is the length of the room,
- $$b$$ is the breadth of the room,
- $$h$$ is the height of the room.

Step 1: Identify the dimensions of the room
- Length (\( l \)) = 8 m
- Breadth (\( b \)) = 5 m
- Height (\( h \)) = 6 m

Step 2: Substitute the values into the formula
Now, we will substitute the values into the diagonal formula:

\( d = \sqrt{8^2 + 5^2 + 6^2} \)

Step 3: Calculate the squares of the dimensions
Calculating the squares:
- \( 8^2 = 64 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)

Step 4: Add the squares together
Now, we add these values together:

\( d = \sqrt{64 + 25 + 36} \)

Calculating the sum:
\( 64 + 25 + 36 = 125 \)

Step 5: Take the square root
Now, we take the square root of 125:

\( d = \sqrt{125} \)

Step 6: Simplify the square root
We can simplify \( \sqrt{125} \):

\( \sqrt{125} = \sqrt{25 \times 5} = 5\sqrt{5} \)

Conclusion
Thus, the length of the largest rod that can be placed in the room is:

\( \text{Length of the rod} = 5\sqrt{5} \text{ meters} \)

Final Answer
The correct option is \( 5\sqrt{5} \).

---