Comprehension :
Consider the following information and answer the questions based on it.
Out of 50 kids in a colony, 10 bike only basketabll, 25 like only football, 10 like both volleyball and football and 5 like only volleyball.
How many kids like only oen sport ?
50
40
35
25
The correct Answer is:D
To solve the problem, we need to determine how many kids like only one sport based on the information provided.
1. Identify the number of kids who like each sport:
- Kids who like only basketball: 10
- Kids who like only football: 25
- Kids who like only volleyball: 5
- Kids who like both volleyball and football: 10
2. Calculate the total number of kids who like only one sport:
- Only basketball: 10 kids
- Only football: 25 kids
- Only volleyball: 5 kids
3. Add the numbers of kids who like only one sport:
Total kids who like only one sport=Only basketball+Only football+Only volleyball
=10+25+5=40
4. Conclusion:
- The total number of kids who like only one sport is 40.
Final Answer:
40 kids like only one sport.
---
- Kids who like only basketball: 10
- Kids who like only football: 25
- Kids who like only volleyball: 5
- Kids who like both volleyball and football: 10
- Only basketball: 10 kids
- Only football: 25 kids
- Only volleyball: 5 kids
Total kids who like only one sport=Only basketball+Only football+Only volleyball
=10+25+5=40
- The total number of kids who like only one sport is 40.
40 kids like only one sport.
Similar Questions
Study the following diagram and answer questions based on it
The ratio of kids who like only Mars to those who like all the three is.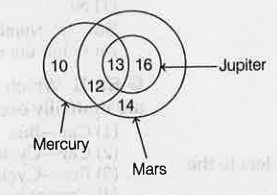
View SolutionConsider the following information and answer the question based on it. In a group of 75 students, 12 like only cabbage, 15 like only cauliflower, 21 like only carrot, 12 like both carrot and cabbage, 13 like only capsicum and 2 like both capsicum and cauliflower : The difference between the people who like carrot and cauliflower is
View Solution
Knowledge Check
Comprehension :
Consider the following information and answer the questions based on it.
Out of 50 kids in a colony, 10 bike only basketabll, 25 like only football, 10 like both volleyball and football and 5 like only volleyball.
The ratio of kids who like football to those who like only basketball isA5/2B7/2C4D5Among 60 students, 12 like only algebra, 13 like only geometry, 10 like only trigonometry, 5 like both algebra and trigonometry, 8 like only physics, 5 like both physics and geometry and the remaining like both algebra and physics. How many students like more than one subject?
AABBCDDCAmong 60 students, 12 like only algebra, 13 like only geometry, 10 like only trigonometry, 5 like both algebra and trigonometry, 8 like only physics, 5 like both physics and geometry and the remaining like both algebra and physics. The ratio of students who like algebra to those who like geometric is
ACBDCADB
Study the following diagram and answer questions based on it
How many people who like Mars like Jupiter also ?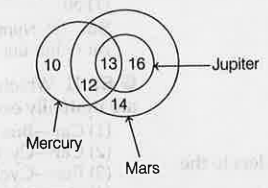
View SolutionAmong 60 students, 12 like only algebra, 13 like only geometry, 10 like only trigonometry, 5 like both algebra and trigonometry, 8 like only physics, 5 like both physics and geometry and the remaining like both algebra and physics. The number of students who like physics but not geometry is
View SolutionComprehension:
Consider the following information and answer the ,questions based on it. In a building, 30 people drink coffee, 40 drink tea, 25 drink both tea and coffee, 20 drink both tea and milk and 15 drink all the three -tea, coffee and milk.
The number of people who drink only coffee is _______ than those who drink all the three (milk, tea & coffee)
View SolutionStudy the infromation carefully and answer the question based on it :
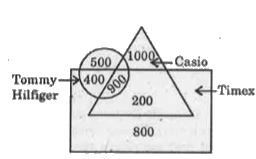
How many persons like only Casio and Timex ?
View SolutionConsider the following information and answer the questions based on it. Out of 60 people in a colony, 10 speak only Bengali, 5 speak only Assamese, 10 speak both Hindi and Odia, 12 speak both Marathi and Hindi, 13 speak English, Tamil and Marathi, 5 speak both Assamese and Hindi and the remaining speak both Bengali and Hindi.
How many people speak more than one language?
A. 15
B. 45
C. 50
D. 55
View Solution
