Let f be function f(x)=cosx−(1−X22).Then
A
f (x)is an increasing function
B
f (x) is decreasing function
C
f(x) is an increasing function in the interval −∞<x≤0 and decreasing in the interval 0≤x<∞
D
f(x) is a decreasing function in the interval −∞<x≤0 and increasing in the interval 0≤x<∞
Video Solution
Text Solution
The correct Answer is:D
f(x) = - sin x +x , we know sin x <x for x>0 and sin x>x for x<0
Thus f(x) > 0 (inc ) for x >0 and f(x) <0 for x <0 (dec)
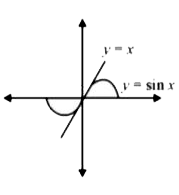
|
Similar Questions
Knowledge Check
Let f be a function defined by
f(x)=(x−1)2+x,(x≥1).
Statement-1: The set [x:f(x)=f−1(x)]={1,2}
Statement-2: f is a bijectioon and f−1(x)=1+√x−1,x≥1A1B2C3D4Let f(x) be the function given by f(x)=arccos(1−x21+x2).Then
Af(x) is everywhere differential such that f'(x)=21+x2Bf'(x)=⎧⎪⎨⎪⎩21+x2x>0−21+x2x<0Cf'(x)=⎧⎪⎨⎪⎩−21+x2x>021+x2x<0Df'(x) exists at x=0Let f(x) be a function given by f(x)=x2+1[x]
where [] denotes the greatest interger function .Then f(x) is monotonicallyAincreasing on [1,4)Bdecreasing [1,4)Cincreasing on [1,2)Ddecreasing on [2,3)
Let f:A→B be an invertible function. If f(x)=2x3+3x2+x−1, then f−1(5)=
View SolutionDiscuss the continuity of the function :
f(x)={1−cosxx2, x≠01, x=0 at x = 0.
View SolutionLet f(x) be a function defined as f(x)={x2−1x2−2|x−1|−1,x≠112,x=1 Discuss the continuity of the function at x=1.
View SolutionLet f:R→R be a function given by f(x)=x2+1. Find: f−1{−5}
View SolutionLet f:(−∞,2]→(−∞,4] be a function defined by f(x)=4x−x2. Then, f−1(x) is
View Solution