The number of points at which the function,
otherwise is not differentiable is:
A
0
B
1
C
2
D
More than 2
Video Solution
Text Solution
The correct Answer is:B
plotting graph of required function
zig-zag curve is the min. curve which is asked in the question
thus it appears that there are 2 pts. of non-differentiability
But at x=1 , L.H.D = 2x = 2 and R.H.D = 2
Thus there is only one pt. of non-differentiability
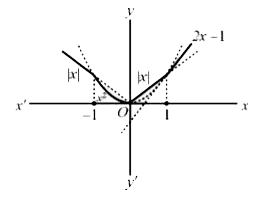
|
Similar Questions
Knowledge Check
Let f(x)=min{x,x2}, for every x∈R. Then
Af (x) is continuous for all xBf (x) is diffentiable for all xCf'(x)=1 for x>1Df (x) is not differentiable at two values of xConsider the function f(x)=min{∣∣x2−9∣∣,∣∣x2−1∣∣}, then the number of points where f(x) is non - differentiable is/are
A0B7C6D4Consider the function f(x)=min{∣∣x2−4∣∣,∣∣x2−1∣∣}, then the number of points where f(x) is non - differentiable is/are
A0B7C6D4
The function f(x)=min{x−[x],−x−|−x|} is a
View SolutionFind the number of critical points of the function
f (x) = min (tan x , cos x) , x∈(0,π)
View SolutionThe total number of points where the function f(x)=|x+2|+|x−1| is not differentiable is
View SolutionIf f(x)={min(x,x2),x≤0andmin(2x,x2−1),x<0, then find the number of non-differentiable points of f(x).
View SolutionThe function f(x)=min{|x|,√1−x2},−1<x<1 possesses
View Solution