For the following questions answer them individually
The time required for a boy to travel along the external and internal boundaries of a circular path are in the ratio 20: 19. If the width of the path be 5 metres, the internal diameter is:
195 metres
192 metres
180 metres
190 metres
The correct Answer is:D
To solve the problem step-by-step, we will follow the logical reasoning laid out in the video transcript.
1. Understand the Problem: We have a circular path with an external and internal boundary. The time taken to travel along these boundaries is in the ratio of 20:19. The width of the path is given as 5 meters. We need to find the internal diameter of the circular path.
2. Define Variables:
- Let the internal radius be r1.
- The external radius will then be r2=r1+5 (since the width of the path is 5 meters).
3. Circumference Calculation:
- The circumference of the external boundary is given by Cexternal=2πr2=2π(r1+5).
- The circumference of the internal boundary is given by Cinternal=2πr1.
4. Set Up the Ratio:
- The ratio of the time taken to travel the external boundary to the internal boundary is given as CexternalCinternal=2019.
- Substituting the circumferences into the ratio gives us:
2π(r1+5)2πr1=2019
- The 2π cancels out, simplifying to:
r1+5r1=2019
5. Cross Multiply:
- Cross multiplying gives:
19(r1+5)=20r1
- Expanding this results in:
19r1+95=20r1
6. Rearranging the Equation:
- Rearranging the equation gives:
95=20r1−19r1
95=r1
7. Calculate the Internal Diameter:
- The internal diameter D is given by D=2r1:
D=2×95=190 meters
Final Answer:
The internal diameter is 190 meters.
---
- Let the internal radius be r1.
- The external radius will then be r2=r1+5 (since the width of the path is 5 meters).
- The circumference of the external boundary is given by Cexternal=2πr2=2π(r1+5).
- The circumference of the internal boundary is given by Cinternal=2πr1.
- The ratio of the time taken to travel the external boundary to the internal boundary is given as CexternalCinternal=2019.
- Substituting the circumferences into the ratio gives us:
2π(r1+5)2πr1=2019
- The 2π cancels out, simplifying to:
r1+5r1=2019
- Cross multiplying gives:
19(r1+5)=20r1
- Expanding this results in:
19r1+95=20r1
- Rearranging the equation gives:
95=20r1−19r1
95=r1
- The internal diameter D is given by D=2r1:
D=2×95=190 meters
The internal diameter is 190 meters.
Similar Questions
The ratio of the outer and the inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is (a) 55 m (b) 110 m (c) 220 m (d) 230 m
View SolutionThe Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level. For the viewer A, the angle of elevation of “D” is double the angle of elevation of “C” The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following:
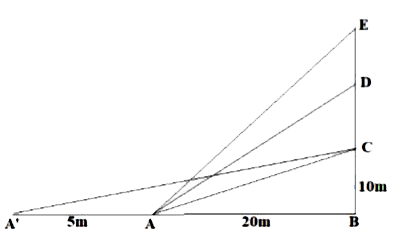
A1 Is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between ∠CAB and ∠CA'B Is
View Solution
Knowledge Check
The ratio of the outer and the inner perimeter of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is :
A110 mB55mC220 mD230 mA path of uniform width surrounds a circular park. The difference of internal and external circumferences of this circular path is 132 metres. Its width is :
(Take π=227)A22 mB20 mC21 mD24 mA path of uniform width surrounds a circular park. The difference of internal and external circumference of this circular path is 132 metres. Its width is :
(Take π=227)A22mB20 mC21mD24m
A circular water fountain 6.6 m in diameter is surrounded by a path of width 1.5 m. The area of this path in square metres is-
View SolutionA model rocket rests on a frictionless horizontal surface and is joined by a string of length l to a fixed point so that the rocket moves in a horizontal circular path of radius l. The string will break if its tensiion exceeds a value T. The rocket engine provides a thrust F of constant magnitude along the rocket's direction of motion. the rocket has a mass m that does not change with time. Answer the following questions based on the above passage.
What distance does the rocket travel between the time t1 when the string breaks and the time 2t1? The rocket engine continues of operate after the string breaks.
View SolutionStudy the following information to
answer the questions given below it.
A number sorting machine, when given an input of
numbers, rearranges the numbers in a particular manner step
by step indicated below-- till all the numbers are arranged in a particular order.
input : 29 2 15 5 20 11 50 105 28 19 30 140Step I : 2 29 15 5 20 11 50 105 28 19 30 140Step II : 2 140 15 5 20 11 50 105 28 19 30 29Step III : 2 140 5 15 20 11 50 105 28 19 30 29Step IV : 2 140 5 105 20 11 50 15 28 19 30 29 Step V : 2 140 5 105 11 20 50 15 28 19 30 29Step VI : 2 140 5 105 11 50 20 15 28 19 30 29Step VII: 2 140 5 105 11 50 15 20 28 19 30 29Step VIII : 2 140 5 11 50 15 30 28 19 20 29Step IX: 2 140 5 105 11 50 15 30 19 28 20 29 Step X: 2 140 5 105 11 50 15 30 19 29 20 28
How many steps would be required in getting the final
output for the following input ?
Input : 10, 4, 1, 9, 8, 12
View SolutionTwo gaseous molecules A and B are traveling towards each other. Let the mean free path of the molecule be σ and Z be the collision number with other molecules at pressure 1atm. Answer the following questions
If Z is the total number of collisions which a gas molecule registers with others per unit time under particular conditions, then the collision frequency of the gas containing N molecules per unit volume is
View SolutionRead the following text and answer the following questions on the basis of the same:
Electromagnetic damping: Take two hollow thin cylindrical pipes of equal internal diameters made of aluminium and PVC, respectively. Fix them vertically with clamps on retort stands.
Take a small cylindrical magnet having diameter slightly smaller than the inner diameter of the pipes and drop it through each pipe in such a way that the magnet does not touch the sides of the pipes during its fall. You will observe that the magnet dropped through the PVC pipe takes the same time to come out of the pipe as it would take when dropped through the same height without the pipe. Now instead of PVC pipe use an aluminium pipe. Note the time it takes to come out of the pipe in each case. You will see that the magnet takes much longer time in the case of aluminium pipe. Why is it so? It is due to the eddy currents that are generated in the aluminium pipe which oppose the change in magnetic flux, i.e., the motion of the magnet.
The retarding force due to the eddy currents inhibits the motion of the magnet. Such phenomena are referred to as electromagnetic damping Note that eddy currents are not generated in PVC pipe as its material is an insulator whereas aluminium is a conductor. This effect was discovered by physicist Foucault (1819-1868).
A piece of wood and a bar magnet of same dimension is dropped through an aluminium pipe. Which of the following statements is true?
View Solution
