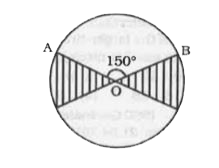
Consider the circle shown below having angle AOB as 135∘ and the shaded portion is the x part of the circular region. Calculate the value of x.

1/12
1/9
1/6
1/4
The correct Answer is:D
Step by step video, text & image solution for Consider the circle shown below having angle AOB as 135^@ and the shaded portion is the x part of the circular region. Calculate the value of x. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Carefully study the circuit diagram shown and calculate the value of x.
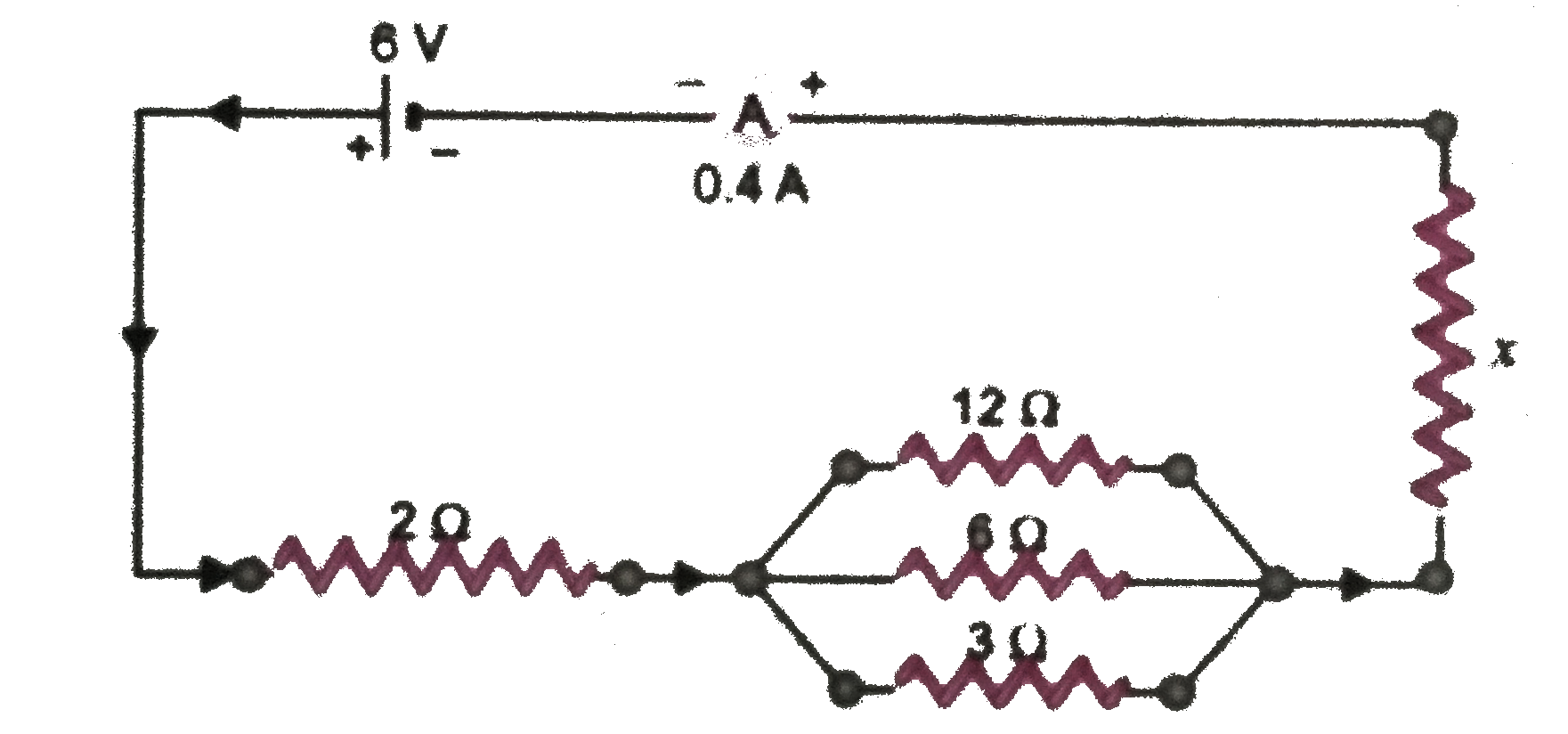 .A14.3 ohmB11.3 ohmC12 ohmD23.4 ohm
.A14.3 ohmB11.3 ohmC12 ohmD23.4 ohm - Question 2 - Select One
In the figure below, the square JKLM is inscribed within a circle and ΔJMN is a right-angled isosceles triangle. The point marked O is the centre of the circle.
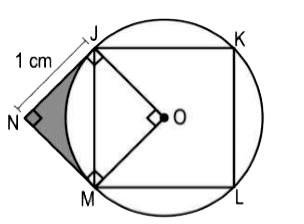
What is the area of the shaded part of the figure?A(π4−12)cm2B(π−12)cm2C(1−π4)cm2D(1−π)cm2 - Question 3 - Select One
The shaded region given below represents the constraints (other than x≥0,y≥0)
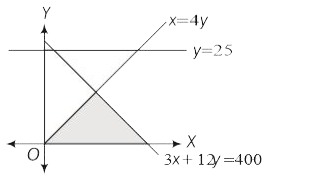 A3x+4y≤400,y≤25,x≤4yB3x+12y≥400,y≤25,x≥4yC3x+12y≤400,y≤25,x≥4yDnone of these
A3x+4y≤400,y≤25,x≤4yB3x+12y≥400,y≤25,x≥4yC3x+12y≤400,y≤25,x≥4yDnone of these
If Figure, there are three semicircles, A, B and C having diameter 3cm each, and another semicircle E having a circle D with diameter 4.5cm are shown. Calculate: the area of the shaded region. the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.
View SolutionAn arc AB of a cricle subtends an angle x radians at the centre O of the circle, Given that the area of the sector AOB is equal to the square of the length of the arc AB, find the volume of x.
View SolutionThe angles of a quadrilateral are in the ratio 3:5:6:10. Then find the angles of the quadrilateral.
View SolutionThe shaded region given below represents the constraints (other than x≥0,y≥0)
 View Solution
View SolutionThere is a circular loop of current of radius , as shown in figure: If current enters at point A and leaves at point B where ∠AOB is 90∘ and the wire of the loop is of uniform cross section area, then calculate the magnetic field intensity at the centre of the loop.
 View Solution
View Solution