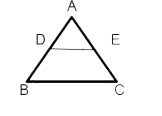
Analyze the figure shown below in which DE || BC and the other dimensions are as follows: AD=3 cm, BD=4 cm, AE=4.4 cm and DE=6 cm. Calculate the length (in cm) of BC.
6
8
12
14
The correct Answer is:A, D
To solve the problem, we will use the properties of similar triangles. Since DE is parallel to BC, triangles ADE and ABC are similar.
1. Identify the lengths given in the problem:
- AD = 3 cm
- BD = 4 cm
- AE = 4.4 cm
- DE = 6 cm
2. Calculate the length of AB:
- Since AB = AD + BD,
- AB = 3 cm + 4 cm = 7 cm.
3. Set up the ratio of the sides of the similar triangles:
- From the similarity of triangles ADE and ABC, we have:
ADAB=DEBC
4. Substitute the known values into the ratio:
- We know AD = 3 cm, AB = 7 cm, and DE = 6 cm.
- Substitute these values into the ratio:
37=6BC
5. Cross-multiply to solve for BC:
- Cross-multiplying gives:
3⋅BC=6⋅7
- This simplifies to:
3⋅BC=42
6. Divide both sides by 3 to find BC:
- Thus,
BC=423=14 cm
Final Answer:
The length of BC is 14 cm.
- AD = 3 cm
- BD = 4 cm
- AE = 4.4 cm
- DE = 6 cm
- Since AB = AD + BD,
- AB = 3 cm + 4 cm = 7 cm.
- From the similarity of triangles ADE and ABC, we have:
ADAB=DEBC
- We know AD = 3 cm, AB = 7 cm, and DE = 6 cm.
- Substitute these values into the ratio:
37=6BC
- Cross-multiplying gives:
3⋅BC=6⋅7
- This simplifies to:
3⋅BC=42
- Thus,
BC=423=14 cm
The length of BC is 14 cm.
Similar Questions
Knowledge Check
- Question 1 - Select One
If in ΔABC,DE∣∣BC,AB=7.5cm,BD=6cm and DE=2cm, then the length of BC in cm is :
A6B8C10D10.5 - Question 2 - Select One
In the given figure AB = 12, AC = 15 cm and AD = 6 cm. BC∣∣DE, find the length of AE
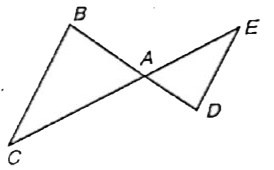 A6 cmB7.5 cmC9 cmD10 cm
A6 cmB7.5 cmC9 cmD10 cm
In the given figure, DE|∣|BC,AD=2cm,BD=2.5cm,AE=3.2cmandDE=4cm. Find AC and BC.
 View Solution
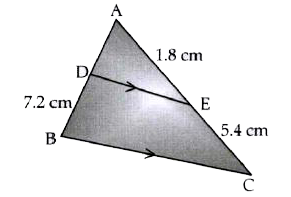
View SolutionIn Figure below DE||BC . Find the length of side AD given that AE =1.8 cm BD = 7.2 cm and CE = 5.4 cm.
 View Solution
View SolutionIn the given figure, DE∣∣BC. Find the length of side AD given that AE=1.8cm,BD=7.2cm and CE=5.4cm.
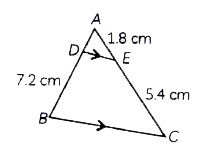 View Solution
View SolutionIn the given figure, DE∣∣BC such that AD=xcm,DB=(3x+4)cmAE=(x+3)cm,andEC=(3x+19)cm. Find the value of x.
 View Solution
View SolutionIn the below figure , AD=18cm,BD=6cmandEC=11cm. If ∠ABE=∠ACD, then find the length of side AE (in cm ).
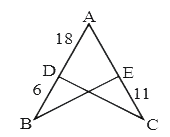 View Solution
View SolutionIn Figure DE|| BC find the length of side AD is ……….. Given that AE = 1.8 cm ,BD = 7.2 cm and CE = 5.4 cm .
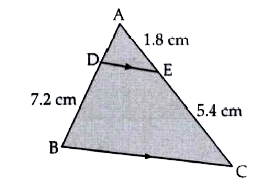 View Solution
View Solution