The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to :
45∘
55∘
60∘
50∘
The correct Answer is:B
To solve the problem, we need to find the value of angle AQP given that angle BAP is 125°.
1. Understanding the Geometry:
- We have a circle with center O and a diameter PQ.
- A tangent at point A intersects the extended diameter PQ at point B.
- We know that angle BAP = 125°.
2. Using the Tangent-Secant Theorem:
- According to the properties of tangents and chords, the angle between the tangent (BA) and the chord (AP) is equal to the angle subtended by the chord (AP) on the opposite side of the tangent.
- Therefore, angle BAP = angle AQP.
3. Finding angle AQP:
- Since angle BAP = 125°, we can conclude that angle AQP also equals 125°.
4. Final Answer:
- Thus, angle AQP = 125°.
- We have a circle with center O and a diameter PQ.
- A tangent at point A intersects the extended diameter PQ at point B.
- We know that angle BAP = 125°.
- According to the properties of tangents and chords, the angle between the tangent (BA) and the chord (AP) is equal to the angle subtended by the chord (AP) on the opposite side of the tangent.
- Therefore, angle BAP = angle AQP.
- Since angle BAP = 125°, we can conclude that angle AQP also equals 125°.
- Thus, angle AQP = 125°.
Similar Questions
The tangent at a point A of a circle with centre O intersects the diameter PQ of the circle (when extended) at the point B. If ∠BAP=125∘, then ∠AQP is equal to:
केंद्र O के साथ एक वृत्त के बिंदु A पर स्पश्रेखा, बिंदु , B पर वृत्त के व्यास PQ ( जब विस्तारित) को काटती है यदि∠BAP=125∘ है, तो ∠AQP के ज्ञात करें ।
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View Solution
Knowledge Check
The tangent at a point A on a circle with center O intersects the diameter PQ of the circle, when extended,at point B. If ∠BAQ=105∘, then ∠APQ is equal to:
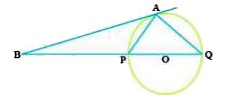 A55∘B60∘C65∘D75∘
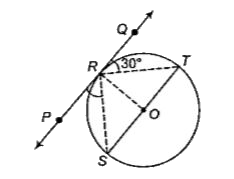
A55∘B60∘C65∘D75∘PQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
A30∘B60∘C45∘D120∘PA and PB are tangents to a circle with centre 0, from a point P outside the circle, and A and B are point on the circle. If ∠APB=30∘, then ∠OAB is equal to:
A25∘B40∘C15∘D50∘
In figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
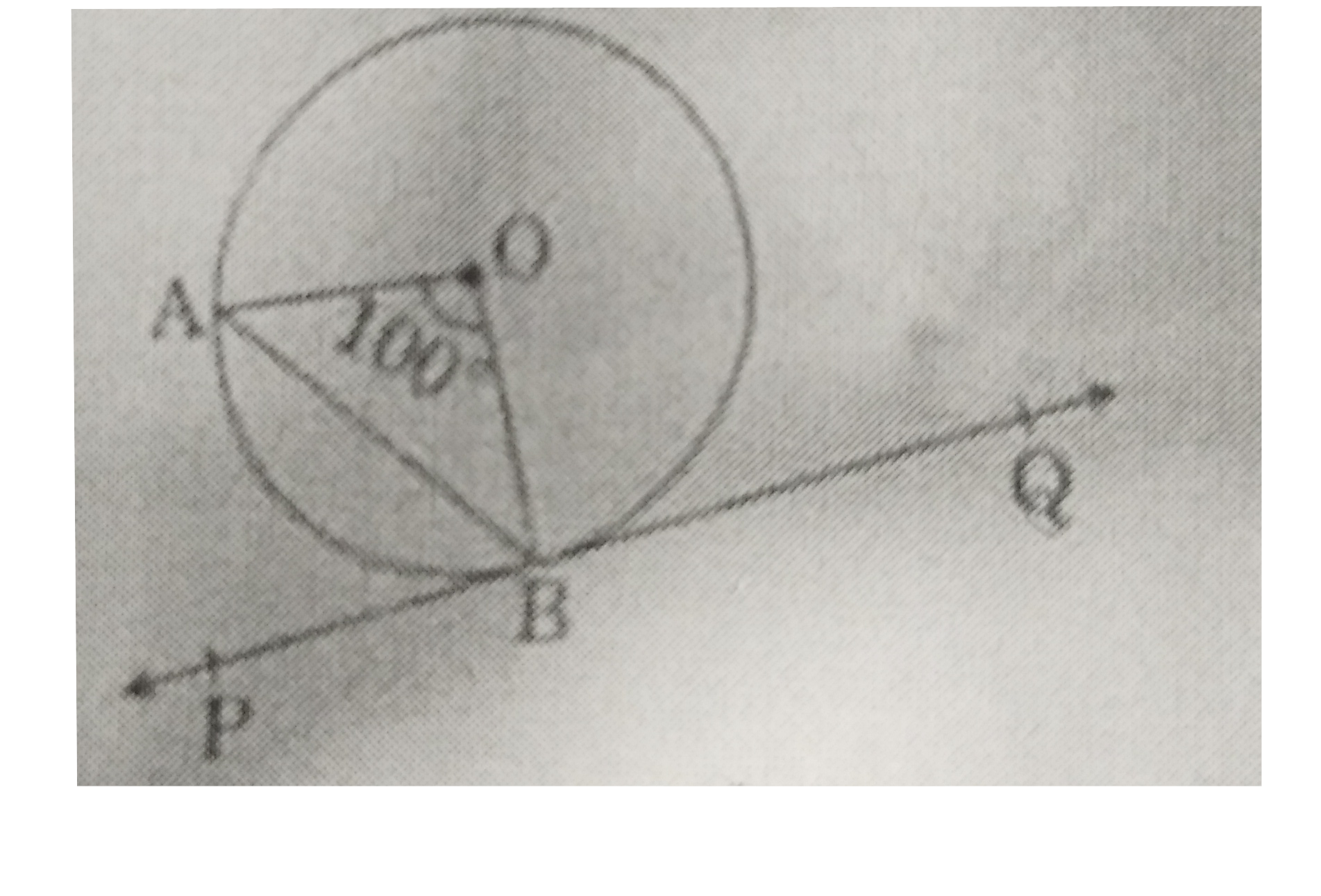
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionThe tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
View Solution
