In a triangle XYZ, L and M are mid points of XY and XZ. R is a point on Side LM such that LR : RM = 1 : 2. If LR = 3cm then the value of YZ is equal to:
19 cm
17 cm
18 cm
16 cm
The correct Answer is:C
Step by step video, text & image solution for In a triangle XYZ, L and M are mid points of XY and XZ. R is a point on Side LM such that LR : RM = 1 : 2. If LR = 3cm then the value of YZ is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
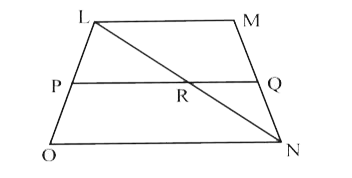
In the figure LMNO, is a trapezium in which LM is parallel to side ON and P is the mid point of side LO. If Q is a point on the side MN such that segment PQ is parallel to side ON Prove that Q is the mid point of MN and PQ=1/2(LM+ON).
View SolutionThree points X,Y, Z are on a straight line such that XY=10 and XZ=3. What is the product of all possible values of YZ?
View Solution
Knowledge Check
The mid-points of AB and AC of a ΔABC are respectively X and Y. If BC + XY = 12 units, then the value of BC - XY is
A6B8C4D12If X,Y and Z are three points such that XY = 2YZ and XZ =3YZ , then the three points are :
Anot collinearBcollinear and X lies between Y and ZCcollinear and Y lies between X and ZDcollinear and Z lies between X and YXYZ is a right angled triangle and ∠Y=90∘. If XY=2.5cm and YZ=6cm then the circumradius of ΔXYZ is :
A6.5 cmB3.25 cmC3 cmD2.5 cm
If the vertex of a triangle is (1 , 1) and the midpoints of two sides of the triangle through this vertex are (-1 , 2 ) and (3 , 2) , then the centroid of the triangle is :
View SolutionThe mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12units, then the value of (BC−XY) is :
View SolutionThe mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12 units, then the value of (BC−XY) is
View SolutionLet X be the midpoint of the side AB of triangle ABC. And Y be the mid point of CX. If Z is the point where BY meets the side AC, then AZ:ZC is equal to
View SolutionIf ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
View Solution
