In a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
4 cm
3√5 cm
5√3cm
5 cm
The correct Answer is:D
Step by step video & text solution for In a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and angle OBA= 60^@. If angle DOC= 60^@, then what is the length of BC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
In a circle with centre O, AD is a diameter and AC is a chord. B is a point on AC, such that OB = 5 cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र O वाले एक वृत्त में, AD व्यास है तथा AC जीवा है | B, AC पर स्थित बिंदु है जो इस प्रकार है कि OB =5 सेमी तथा ∠OBA=60∘ है | यदि ∠DOC=60∘ है, तो BC की लंबाई ज्ञात करें |
View SolutionIn a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View Solution
Knowledge Check
In a circle with centre O, AOC is a diameter of the circle, BD is a chord and OB and CD are joined. If ∠AOB =130∘, then ∠BDC is equal to
A30∘B25∘C50∘D60∘AC is a chord of that circle whose center is 'O'. If B is any point on arc AC and ∠OCA=20∘, then what is the measurement of ∠ABC ?
A100∘B40∘C140∘D110∘In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
A2ABB√2ABC12ABD1√2AB
AC=25 and D is a point on BC such that AD is the bisector of angle A, as shown in the figure. What is the length of AD?
View SolutionThe radius of a circle is 8 cm and O is its centre. If ∠AOB=60∘ and AB is a chord, then what is the length of the chord AB?
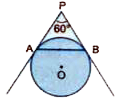
View SolutionIn Fig AP and BP are tangents to a circle with centre O, such that AP = 5 cm , and ∠APB=60∘ . Find the length of chord AB.
View SolutionIn a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
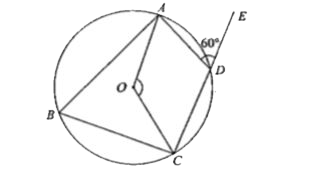
View SolutionIf O is the centre of circle and ∠ADE=60∘ then find ∠AOC
View Solution
