Consider the following statements :
1. If G is the centroid of triangle ABC, then GA=GB=GC.
2. If H is the orthocentre of triangle ABC, then HA=HB=HC.
Which of the statements given above is/are correct ?
1 only
2 only
Both 1 and 2
Neither 1 nor 2
To solve the problem, we need to analyze the two statements regarding the properties of the centroid and orthocenter of triangle ABC.
Step 1: Analyze Statement 1
- Statement 1 claims that if G is the centroid of triangle ABC, then GA = GB = GC.
- The centroid of a triangle is the point where the three medians intersect. It divides each median in a 2:1 ratio.
- The distances from the centroid to the vertices (GA, GB, GC) are not necessarily equal unless triangle ABC is equilateral.
- Therefore, Statement 1 is not universally true.
Step 2: Analyze Statement 2
- Statement 2 claims that if H is the orthocenter of triangle ABC, then HA = HB = HC.
- The orthocenter is the point where the three altitudes of the triangle intersect.
- Similar to the centroid, the distances from the orthocenter to the vertices (HA, HB, HC) are not equal unless triangle ABC is equilateral.
- Therefore, Statement 2 is also not universally true.
Step 3: Conclusion
- Since both statements are only true for equilateral triangles and no condition is given that triangle ABC is equilateral, both statements are incorrect.
- Thus, the answer to the question is that neither statement 1 nor statement 2 is correct.
Final Answer: Neither statement 1 nor statement 2 is correct.
---
- Statement 1 claims that if G is the centroid of triangle ABC, then GA = GB = GC.
- The centroid of a triangle is the point where the three medians intersect. It divides each median in a 2:1 ratio.
- The distances from the centroid to the vertices (GA, GB, GC) are not necessarily equal unless triangle ABC is equilateral.
- Therefore, Statement 1 is not universally true.
- Statement 2 claims that if H is the orthocenter of triangle ABC, then HA = HB = HC.
- The orthocenter is the point where the three altitudes of the triangle intersect.
- Similar to the centroid, the distances from the orthocenter to the vertices (HA, HB, HC) are not equal unless triangle ABC is equilateral.
- Therefore, Statement 2 is also not universally true.
- Since both statements are only true for equilateral triangles and no condition is given that triangle ABC is equilateral, both statements are incorrect.
- Thus, the answer to the question is that neither statement 1 nor statement 2 is correct.
Similar Questions
Knowledge Check
Consider the following statements
I. If G is the centroid of ΔABC, then
GA = GB = GC.II. If H is the orthocentre of ΔABC, then HA = HB = HC.
Which of the statements given above is/are correct ?AOnly IBOnly IICBoth I and IIDNeither I nor IIIf G is the centroid of a triangle ABC, then GA + GB + GC equals to
A0B3 GAC3 GBD3 GCO is the Ortho centre of ΔABC then A will be Orthocentre
AΔABEBΔBOCCΔOBFDΔOBD
In the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that ∠DAC=∠DCA.
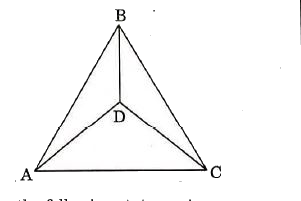
Consider the following statements :
1. Triangle ADC is an isosceles triangle.
2. Dis the centroid of the triangle ABC.
3. Triangle ABD is congruent to the triangle CBD.
Which of the above statements are correct ?
View SolutionIn the triangle ABC,BD=DE=EC,CF=FAandAG=GB Which one of the following statements is not correct
View SolutionIf G is the centroid of triangle ABC,then→GA+→GB+→GC is equal to a. →0 b. 3→GA c. 3→GB d. 3→GC
View SolutionP is the incentre of Δ ABC. Which of the following statements is true ?
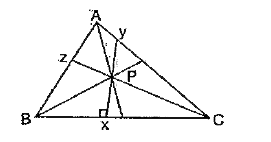
View SolutionIn a triangle ABC, if AB,BC and AC are the three sides of the triangle, then which of the statements is necessarily?
View Solution
