A 5 cm long perpendicular is drawn from the centre of a circle to a 24 cm long chord. Find the diameter of the circle.
A) 26 cm
B) 32 cm
C) 13 cm
D) 30 cm
The correct Answer is:A
Step by step video, text & image solution for A 5 cm long perpendicular is drawn from the centre of a circle to a 24 cm long chord. Find the diameter of the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A chord of length 6 cm is 4 cm away from the centre of circle. Find the diameter of the circle.
A10 cmB6 cmC5 cmD8 cmLength of a tangent segment drawn from a point which is at a distnace 12.5 cm from the centre of a circle is 12cm , find the diameter of the circle.
A25 cmB24 cmC7 cmD14 cmThe radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length is
A√5 cmB2√5 cmC2√7 cmD√7 cm
The radius of a circle is 10 cm and the perpendicular form the centre to a chord is 8cm. Find the length of the chord.
(ii) The radius of a circle is 10 cm. its one chord is 16 cm long. Find the perpendicular distance of this chord form the centre.
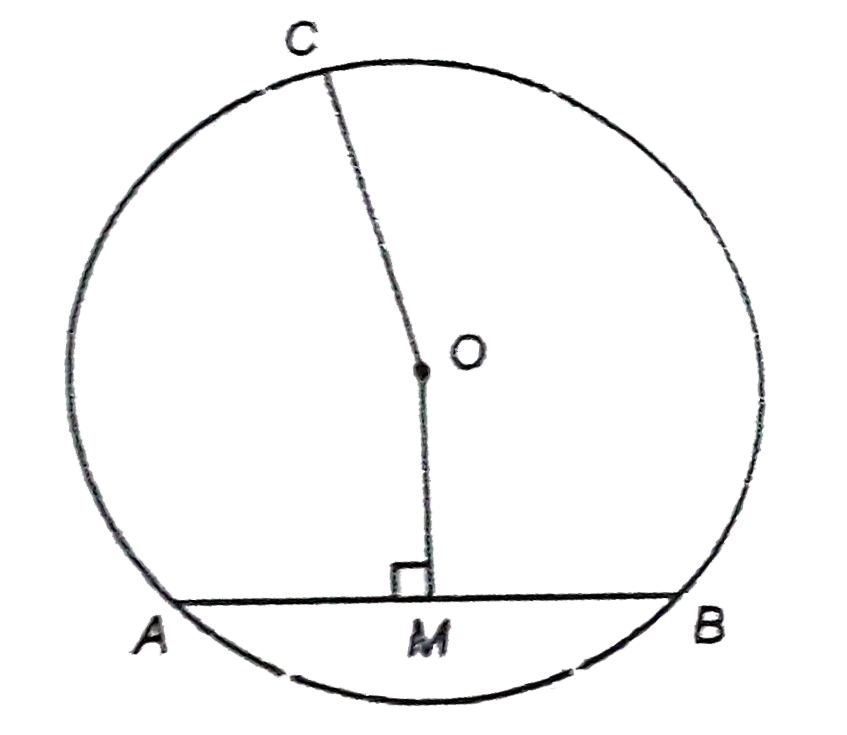
(iii) in the adjoining figure O is the centre of circle. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
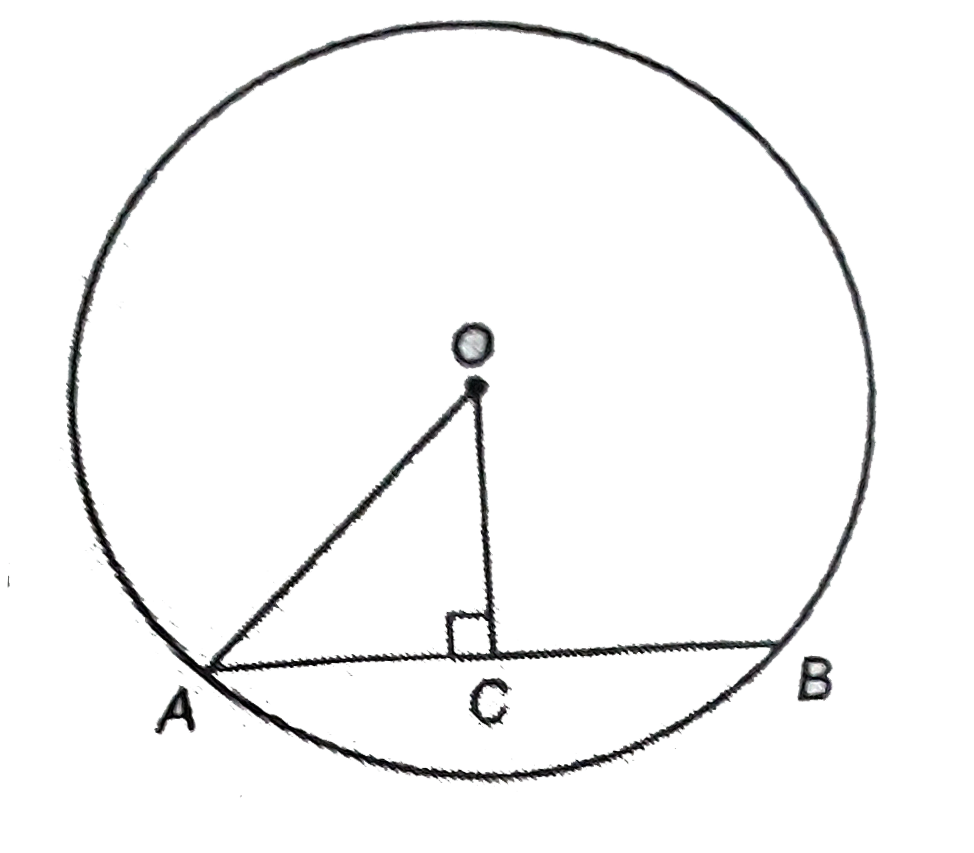
(iv) In the adjoining figure, OM⊥AB, radius OC=5cm and chord AB=8cm.Find the length of OM.
View SolutionA chord of length 30cm is drawn at a distance of 8 cm from the centre of a circle. Find out the radius of the circle.
View SolutionThe length of a chord of a circle is 16 cm and distance of chord is 15 cm from the center of the circle then find the radius of the circle.
View SolutionThe length of the chord of a circle is 8 cm and perpendicular distance between centre and the chord is 3 cm. Then the radius of the circle is equal to :
View SolutionThree circles of diameter 24 cm each touch each other externally. Find the shortest distance from the centre of one circle to the line joining the centres of the other two circles. (in cm.)
View Solution
