The distance between points P and Q is 485 km. If a person starts from point P with the speed of 60 km/h and another person is running with a certain speed from point Q and they both meet after 2.5 hours then find the speed of the person who starts from point Q
140 km/h
126 km/h
156 km/h
134 km/h
The correct Answer is:D
To find the speed of the person who starts from point Q, we can follow these steps:
Step 1: Understand the Problem
We have two points, P and Q, with a distance of 485 km between them. One person starts from point P at a speed of 60 km/h, while another person starts from point Q at an unknown speed. They meet after 2.5 hours.
Step 2: Calculate the Distance Covered by the Person from Point P
The distance covered by the person starting from point P can be calculated using the formula:
Distance=Speed×Time
For the person at point P:
Distance from P=60 km/h×2.5 hours=150 km
Step 3: Calculate the Remaining Distance
Since the total distance between P and Q is 485 km, we can find the distance covered by the person from point Q:
Distance from Q=Total Distance−Distance from P
Distance from Q=485 km−150 km=335 km
Step 4: Calculate the Speed of the Person from Point Q
Now, we can find the speed of the person from point Q using the distance they covered and the time taken:
Speed of Q=Distance from QTime
Speed of Q=335 km2.5 hours
Step 5: Perform the Calculation
Calculating the speed:
Speed of Q=335÷2.5=134 km/h
Conclusion
The speed of the person who starts from point Q is 134 km/h.
---
We have two points, P and Q, with a distance of 485 km between them. One person starts from point P at a speed of 60 km/h, while another person starts from point Q at an unknown speed. They meet after 2.5 hours.
The distance covered by the person starting from point P can be calculated using the formula:
Distance=Speed×Time
For the person at point P:
Distance from P=60 km/h×2.5 hours=150 km
Since the total distance between P and Q is 485 km, we can find the distance covered by the person from point Q:
Distance from Q=Total Distance−Distance from P
Distance from Q=485 km−150 km=335 km
Now, we can find the speed of the person from point Q using the distance they covered and the time taken:
Speed of Q=Distance from QTime
Speed of Q=335 km2.5 hours
Calculating the speed:
Speed of Q=335÷2.5=134 km/h
The speed of the person who starts from point Q is 134 km/h.
Similar Questions
The distance between two points (A and B is 110 km. X starts running from point A at a speed of 60 km/hr and Y starts running from point B at a speed of 50 km/hr at the same time. They meet at a point C, somewhere on the line AB. What is the ratio of AC to BC?
View SolutionA starts from point x at a speed of 15 km/hr and B starts towards A from point y at a speed of 25 km/hr and meet each other after 2 hours at point z. Find the difference in distance between point xz and point yz.
View Solution
Knowledge Check
A person starts from a point P and travels along a path PQRS as shown in the figure, then speed of the person is _____ ms−1
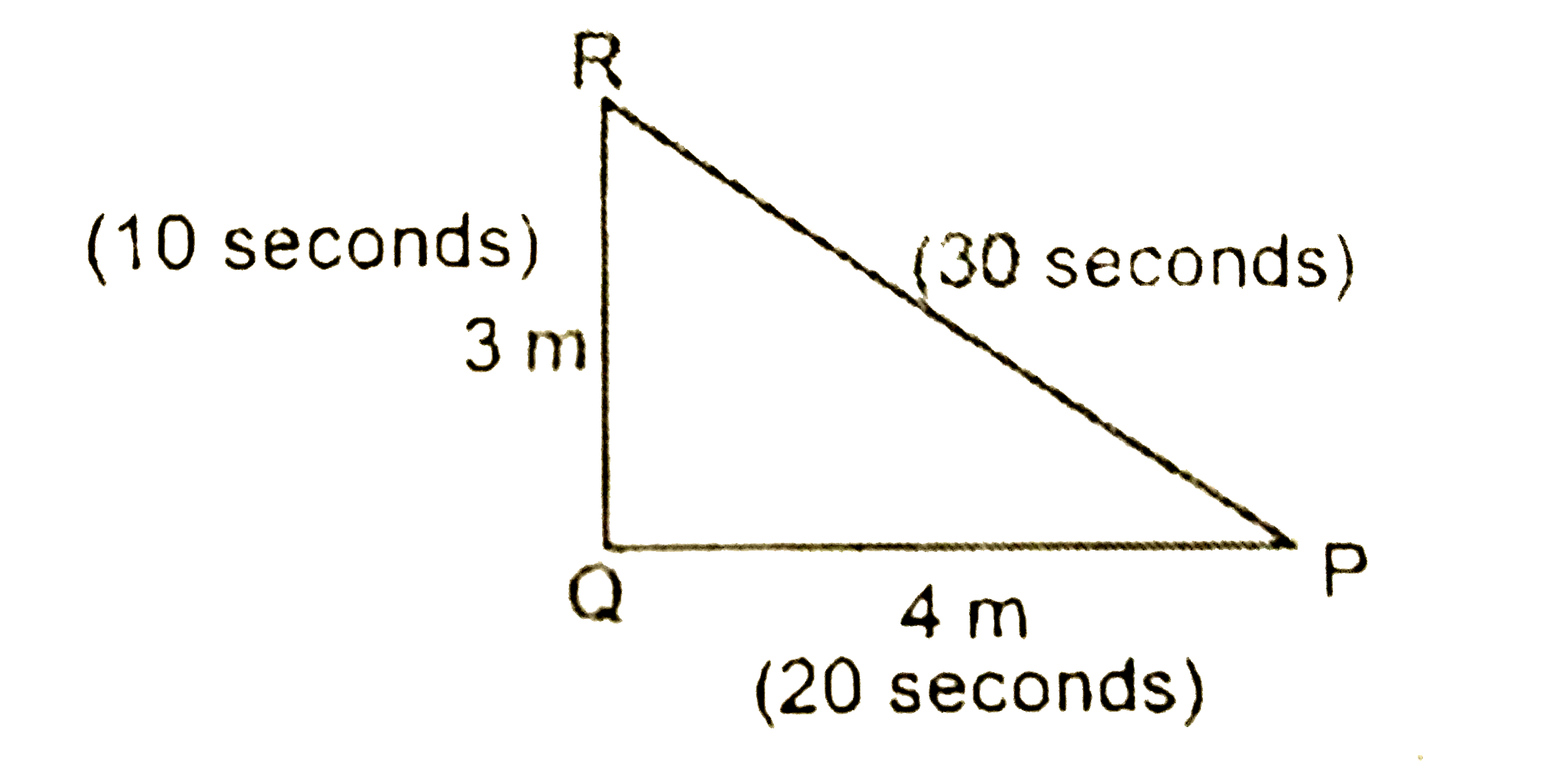 A0.2B20C12D0.4
A0.2B20C12D0.4A person starts from a point P and travels along a path PQRS as shown in the figure, then speed of the person is _____ ms−1
 A0.2B20C12D0.4
A0.2B20C12D0.4A person goes from one point to another point with a speed of 5km/h and comes back to starting point with a speed of 3 km/h. Find the average speed for the whole journey.
A4.5 km/hB4 km/hC4.25 km/hD3.75 km/h
The distance between two places P and Q is 700 km. Two persons A and B started towards Q and P from P and Q simultaneously . The speed of A is 30 km/h and speed of B is 40 km/h. They meet a point M which lies on the way from P to Q.What is the ratio of time taken by A and B to reach their respective destination after meeting at M.
View SolutionThe distance between two places P and Q is 700 km. Two persons A and B started towards Q and P from P and Q simultaneously . The speed of A is 30 km/h and speed of B is 40 km/h. They meet a point M which lies on the way from P to Q.What is the distance MQ.
View SolutionThe distance between two places P and Q is 700 km. Two persons A and B started towards Q and P from P and Q simultaneously . The speed of A is 30 km/h and speed of B is 40 km/h. They meet a point M which lies on the way from P to Q.How long will it take to separate them by 280 km from each other when they cross M (time to be considered after their meeting)?
View SolutionFrom point P, at 6 : 30 pm, a train starts moving towards Q with the speed of 40 km/hr. Another train starts moving from point Q at 7:30 p.m. towards point P at the speed of 60 km/hr. Both of them meet at 11:30 p.m. at point R. What is the ratio of PR and QR?
View SolutionA person goes from point A to B with a speed of 55 km/hr and returns back with a speed 65 km/hr. What is the average speed (in km/hr) of the person while going and coming back from A to B?
View Solution