A glass capillary sealed at the upper end is length and internal diameter . The tube is immersed vertically into a liquid of surface tension . To what length has the capillary to be immersed so that the liquid level inside and outside the capillary becomes the same ? What will happen to the water level inside the capillary if the seal is now broken ?
If A is the crss-sectional area of the tube and L its length, the initial volume of air inside it will be while pressure atmospheric pressure.
Now when the tube is immersed in water its length x in water, the level of water inside and outside is same, so the volume of air in the tube will be . Further if is the pressure of gas in the tube,
i.e.,
Now if temperature is constant,
or
i.e., or
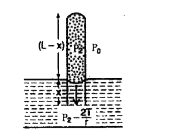
If the seal is broken the pressure inside the capillary will become atmospheric i.e., while capillarity will take place and the rise will be
However, the length of the tube outside the water is , so the tube will be of insufficient length and so the liquid will rise to the top of the tube and will stay there with radius of meniscus,
Similar Questions
A glass capillary sealed at the upper end is of length 0.11m and internal diameter 2×105m. The tube is immersed vertically into a liquid of surface tension 5.06×10−2N/m. To what length the capillary has to be immersed so that the liquid level inside and outside the capillary becomes the same. What will happen to water level inside the capillary if the seal is now broken?
View SolutionA glass capillary sealed at the upper end is of length 0.11m an internal diameter 2×105m. The tube is immersed vertically into a liquid of surface tension 5.06×10−N/m. To what length the capillary has to be immersed so that the liquid level inside and outside the capalliary becomes the same. What will happen to water level inside the capillary if the seal is now broken?
View Solution
Knowledge Check
A galss capillary length l=11cm and inside diameter d=20μm is submerged vertically into water. The upper end of the capillary is sealed. The outside pressure is considered to be 1×105Nm2 . To what length has the capillary to be submerged to make the water levels inside and outside the capillary coincide?
A1.2 cmB2.4 cmC1.4 cmD2.8 cmA glass capillary of length l and inside radius r(r<<l) is submerged vertically into water. The upper end of the capillary is scaled. The atmospheric pressure is p0. To what length h has the capillary to be submerged to make the water levels inside and outside the capillary coincide. Assume that temperature of air in the capillary remains constant. (given, surface tension of water = T, angle of contact between glass water interface =0∘)
 Al1+p0rTBl1+p0r2TCl1+p0r4TDl1+2p0rT
Al1+p0rTBl1+p0r2TCl1+p0r4TDl1+2p0rTThe capillary rises are found to be in the ration of 3:2 when two capillary tubes are immersed in water of surface tension 7.2×10−2 N/m . The ratio of the bore diameters of the capillary tubes is
A2:3B3:2C4:9D9:4
A glass capillary of length l and inside radius r(r<<l) is submerged vertically into water. The upper end of the capillary is scaled. The atmospheric pressure is p0. To what length h has the capillary to be submerged to make the water levels inside and outside the capillary coincide. Assume that temperature of air in the capillary remains constant. (given, surface tension of water = T, angle of contact between glass water interface =0∘)

View SolutionA capillary tube of inside diameter 1 mm is dipped vertically in a liquid of surface tension 63×10−3N/m and density 1262kgm3. Find the height of the capillary rise if the angle of contact is 10∘.
View SolutionA capillary tube of length 12 cm and inside diameter 0.033m is dipped vertically into water. The top end of the capillary is sealed. If the outside pressure is 1.01×105N/m2. Find the length to which the capillary tube should be submerged in water so that the levels inside the outside coincide. σ=72×10−3N/m.
View SolutionA capillary tube is placed vertically inside the beaker of water of surface tension 7×10−2 N/m and the angle of contact is 0∘ . The height raised by the water in capillary tube 7×10−2 m
The radius of the capillary tube is
View SolutionA capillary tube of internal radius 2×10−3 m immersed vertically in beaker containing a liquid rising in the capillary tube is 9×105 kg , the surface tension of the liquid is
View Solution

