An insect flies from the corner A to corner B of a cubic room in 4 second where A and B are diagonally apposite corners. The side of the room is 4 m. The speed of the insect is
√3 m/sec
2√3 m/sec
√2 m/sec
2√2 m/sec
The correct Answer is:A
To find the speed of the insect flying from corner A to corner B of a cubic room, we can follow these steps:
Step 1: Identify the given values
- The side length of the cubic room (A) = 4 m
- Time taken to fly from A to B = 4 seconds
Step 2: Calculate the diagonal distance (d) from corner A to corner B
The formula for the diagonal distance (d) of a cube is given by:
d=√3×A
Substituting the value of A:
d=√3×4
d=4√3 meters
Step 3: Use the formula for speed
The formula for speed (v) is:
v=distancetime
Substituting the values we have:
v=4√34
Step 4: Simplify the speed calculation
v=√3 meters per second
Final Answer
The speed of the insect is √3 meters per second.
---
- The side length of the cubic room (A) = 4 m
- Time taken to fly from A to B = 4 seconds
The formula for the diagonal distance (d) of a cube is given by:
d=√3×A
Substituting the value of A:
d=√3×4
d=4√3 meters
The formula for speed (v) is:
v=distancetime
Substituting the values we have:
v=4√34
v=√3 meters per second
The speed of the insect is √3 meters per second.
Topper's Solved these Questions
Similar Questions
An insect moves with a constant velocity v from one corner of a room to other corner which is opposite of the first corner along the largest diagonal of room.If the insect can not fly and dimensions of a room is a x a x a then the minimum time in which the insect can move is a/v times the square root of a number n then n is equal to?
View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
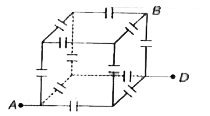
View Solution
Knowledge Check
An insect fly start from one corner of a cubical room and reaches at diagonally opposite corner. The magnitude or displacement of the insect is 40√3 ft. Find the volume of cube.
A64√3ft3B1600ft3C64000ft3DNone of theseA sqaure of side 4 cm is inscirbed in a circular quadrant such that one of the corners of the square coincides with the centre of the quadrant and the diagonally opposite corner lies on the periphery of the quadrant. The area of the quadrant not covered by the square is
A8(π−2)B4(π−2)C8(π−1)D4(π−1)A room has dimensions 3m×4m×5m. A fly starting at one corner ends up at the diamertrically opposite corner. The magnitude of the displacement of the fly is
A12mB60mC2√5mD5√2m
An elephant of length 4 m is at one corner of a rectangular cage of side (16m×30m) and faces towards the diagonally opposite corner. If the elephant starts moving towards the diagonally opposite corner it takes 15 seconds to reach this corner. Find the speed of the elephant.
View SolutionA cubical room has dimensions 4ft×4ft×4ft . An insect starts from one corner O and reaches a corner on the opposite side of the body diagonal.
Suppose that insect does not fly but crawls. Find the minimum distance travelled by insect to reach the destination.
View SolutionAn ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is
View SolutionAn elephant of length 4 m is at one corner of a rectangular cage of side (16m×30m) and faces towards the diagonally opposite corner. If the elephant starts moving towards the diagonally opposite corner it takes 15 seconds to reach this corner. Find the speed of the elephant.
View SolutionAn elephant of length 4 m is at one corner of a rectangular cage 16m×30m and facing towards the diagonally opposite corner . If the elephant starts moving towards the diagonally opposite corner it takes 15 second to reach the opposite corner. Find the speed of the elephant :
View Solution
