How many tangents can be drawn from the poin (3,-2) to the circle x2+y2−8x−6y+9=0?
2
1
0
None of these
The correct Answer is:A
To determine how many tangents can be drawn from the point (3, -2) to the circle given by the equation x2+y2−8x−6y+9=0, we will follow these steps:
Step 1: Rewrite the Circle's Equation in Standard Form
The given equation of the circle is:
x2+y2−8x−6y+9=0
We can rewrite this equation in standard form by completing the square for x and y.
1. Group the x and y terms:
(x2−8x)+(y2−6y)+9=0
2. Complete the square:
- For x2−8x:
x2−8x=(x−4)2−16
- For y2−6y:
y2−6y=(y−3)2−9
3. Substitute back into the equation:
(x−4)2−16+(y−3)2−9+9=0
Simplifying gives:
(x−4)2+(y−3)2−16=0
Thus, we have:
(x−4)2+(y−3)2=16
This represents a circle with center (4,3) and radius 4.
Step 2: Calculate the Distance from the Point to the Center of the Circle
Next, we find the distance d from the point (3,−2) to the center of the circle (4,3) using the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates:
d=√(4−3)2+(3−(−2))2
Calculating this gives:
d=√(1)2+(3+2)2=√1+52=√1+25=√26
Step 3: Compare the Distance to the Radius
Now, we compare the distance d to the radius r of the circle:
- Radius r=4
- Distance d=√26≈5.1
Since d>r, the point (3,−2) lies outside the circle.
Step 4: Determine the Number of Tangents
If a point lies outside a circle, two tangents can be drawn from that point to the circle. Thus, the number of tangents that can be drawn from the point (3,−2) to the circle is:
Number of tangents=2
Final Answer
The answer is that 2 tangents can be drawn from the point (3, -2) to the circle.
---
The given equation of the circle is:
x2+y2−8x−6y+9=0
We can rewrite this equation in standard form by completing the square for x and y.
(x2−8x)+(y2−6y)+9=0
- For x2−8x:
x2−8x=(x−4)2−16
- For y2−6y:
y2−6y=(y−3)2−9
(x−4)2−16+(y−3)2−9+9=0
Simplifying gives:
(x−4)2+(y−3)2−16=0
Thus, we have:
(x−4)2+(y−3)2=16
This represents a circle with center (4,3) and radius 4.
Next, we find the distance d from the point (3,−2) to the center of the circle (4,3) using the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates:
d=√(4−3)2+(3−(−2))2
Calculating this gives:
d=√(1)2+(3+2)2=√1+52=√1+25=√26
Now, we compare the distance d to the radius r of the circle:
- Radius r=4
- Distance d=√26≈5.1
If a point lies outside a circle, two tangents can be drawn from that point to the circle. Thus, the number of tangents that can be drawn from the point (3,−2) to the circle is:
The answer is that 2 tangents can be drawn from the point (3, -2) to the circle.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The number of tangents that can be drawn from the point (8,6) to the circle x2+y2−100=0 is
A0B1C2DnoneThe number of real tangents that can be drawn from (2, 2) to the circle x2+y2−6x−4y+3=0, is
A0B1C2D3
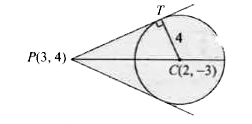
Find the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
View SolutionIf two perpendicular tangents can be drawn from the origin to the circle x2−6x+y2−2py+17=0 , then the value of |p| is___
View SolutionIf tangents are drawn from origin to the circle x2+y2−2x−4y+4=0, then
View SolutionThe number of tangents that can be drawn from (0, 0) to the circle x2+y2+2x+6y−15=0
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View SolutionThe length of the tangent drawn from the point (2,3) to the circle 2(x2+y2)−7x+9y−11=0.
View Solution

