Suppose ABC is a right angled triangle with right angled at C . If length of sides opposite to angle A,B,C are respectively u,v and w then tanA+tanB equals
u2uv
1
u+v
w2uv
The correct Answer is:D
To solve the problem, we need to find the value of tanA+tanB for a right-angled triangle ABC, where the right angle is at C, and the sides opposite to angles A, B, and C are u, v, and w respectively.
1. Identify the Triangle and Angles:
- We have a right-angled triangle ABC with right angle at C.
- The sides opposite to angles A, B, and C are u, v, and w respectively.
- Thus, AC=v (base), BC=u (perpendicular), and AB=w (hypotenuse).
2. Write the Expressions for tanA and tanB:
- The tangent of an angle in a right triangle is defined as the ratio of the opposite side to the adjacent side.
- For angle A:
tanA=Opposite to AAdjacent to A=uv
- For angle B:
tanB=Opposite to BAdjacent to B=vu
3. Add the Tangents:
- Now, we need to find tanA+tanB:
tanA+tanB=uv+vu
4. Combine the Fractions:
- To add these fractions, we need a common denominator:
tanA+tanB=u2+v2uv
5. Use the Pythagorean Theorem:
- In a right triangle, by the Pythagorean theorem, we have:
w2=u2+v2
- Thus, we can substitute u2+v2 with w2:
tanA+tanB=w2uv
6. Final Result:
- Therefore, the final expression for tanA+tanB is:
tanA+tanB=w2uv
- We have a right-angled triangle ABC with right angle at C.
- The sides opposite to angles A, B, and C are u, v, and w respectively.
- Thus, AC=v (base), BC=u (perpendicular), and AB=w (hypotenuse).
- The tangent of an angle in a right triangle is defined as the ratio of the opposite side to the adjacent side.
- For angle A:
tanA=Opposite to AAdjacent to A=uv
- For angle B:
tanB=Opposite to BAdjacent to B=vu
- Now, we need to find tanA+tanB:
tanA+tanB=uv+vu
- To add these fractions, we need a common denominator:
tanA+tanB=u2+v2uv
- In a right triangle, by the Pythagorean theorem, we have:
w2=u2+v2
- Thus, we can substitute u2+v2 with w2:
tanA+tanB=w2uv
- Therefore, the final expression for tanA+tanB is:
tanA+tanB=w2uv
Topper's Solved these Questions
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBook:LUCENT PUBLICATIONChapter:TRIGONOMETRIC RATIO OF SPECIFIC ANGLESExercise:Exercise 10B
Explore 10 Videos
- TRIGONOMETRIC RATIO OF SPECIFIC ANGLESBook:LUCENT PUBLICATIONChapter:TRIGONOMETRIC RATIO OF SPECIFIC ANGLESExercise:Exercise 10B
Explore 10 Videos
- QUADRILATERAL Book:LUCENT PUBLICATIONChapter:QUADRILATERAL Exercise:Exercise 7B
Explore 6 Videos
Similar Questions
Knowledge Check
ABC is a right angled triangle. B being the right angle. Mid-points of BC and AC are respectively B' and A'. Area of ΔA'B'C' is
A12×area of ΔABCB23×area of ΔABCC14×area of ΔABCD18×area of ΔABCABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
A30 unitB20 unitC40 unitDNone of theseABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
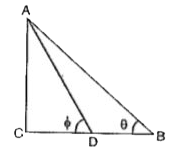 A1B1√2C12D2
A1B1√2C12D2
if in triangle ABC right angled at C then tanA+tanB
View SolutionIf △ABC is a right angled at C, then tanA + tan B equals
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
View SolutionLet triangle ABC be right angled at C.If tanA+tanB2, then-
View Solution
