Given that A + B = R and A = B = R. What should be the angle between A and B ?
0
π/3
2π/3
π
The correct Answer is:C
Step by step video, text & image solution for Given that A + B = R and A = B = R. What should be the angle between A and B ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Find R≠t between A and B.
 View Solution
View SolutionGiven that A=B. What is the angle between (→A+→B)and(→A−→B) ?
View SolutionGiven that A=B. What is the angle between (→A+→B) and (→A−→B) ?
View SolutionGiven that →A+→B=→RandA20+B2−R2, find the angle between →Aand→B .
View SolutionFor what angle between →a and →b, ∣∣→a+→b∣∣=∣∣→a−→b∣∣ .
View SolutionIf →R=→A−→B , and θ is the smaller angle between →A and →B , show that ltbRgt R2=A2+B2−2ABcosθ.
View SolutionA parallelogram is constructed on the vectors r1=3a−b,r2=a+3b, If |a|=|b|=2 and the angle between a and b is π3, then the length of a diagonal of the parallelogram is
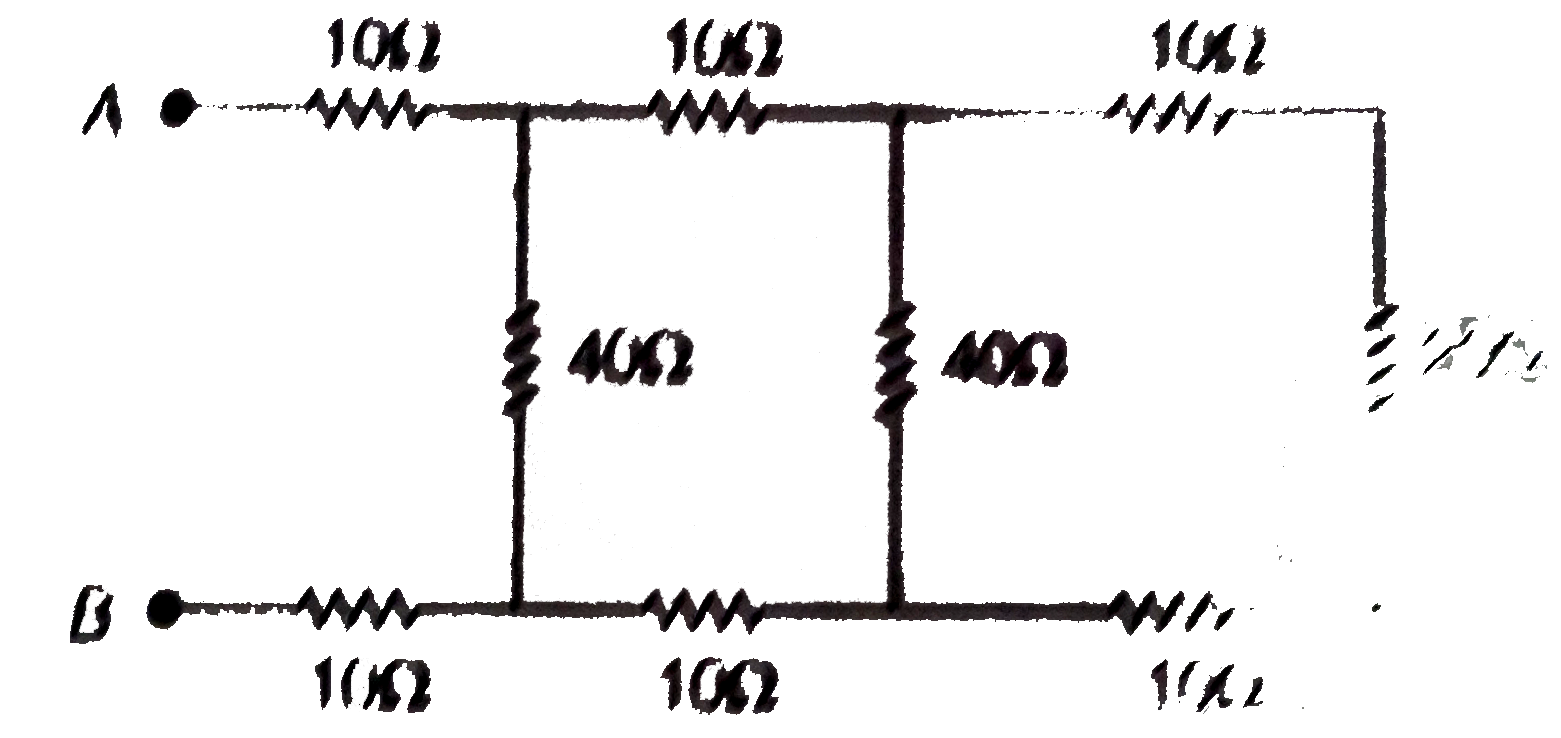
View SolutionIf each of the resistances in the shown network is R, then what is the resistance between A and B.
View SolutionA*B means A is the siste of B
A÷B means A is the brother of B
A+B means A is the father of B
A-B means A is the mother of B
What is the relation between Q and S in 'P+Q÷R−S'View SolutionA*B means A is the siste of B
A÷B means A is the brother of B
A+B means A is the father of B
A-B means A is the mother of B
What is the relation between T and Q in 'P∗Q÷R+S∗T'View Solution


