The angular size of the central maxima due to a single slit diffraction is (a → slit width)
λa
2λa
3λ2a
λ2a
The correct Answer is:B
To find the angular size of the central maxima due to single slit diffraction, we can follow these steps:
1. Understanding Single Slit Diffraction:
In single slit diffraction, light passing through a narrow slit creates a pattern of bright and dark fringes on a screen. The central maximum is the brightest part of the pattern, and it is flanked by dark minima.
2. Identifying the First Minimum:
The position of the first minimum in the diffraction pattern is given by the condition:
Asinθ=λ
where:
- A is the width of the slit,
- λ is the wavelength of the light,
- θ is the angle at which the first minimum occurs.
3. Finding sinθ:
Rearranging the equation gives:
sinθ=λA
4. Small Angle Approximation:
For small angles, we can use the approximation sinθ≈θ (in radians). Thus, we have:
θ≈λA
5. Calculating the Angular Size of the Central Maxima:
The angular size of the central maximum is defined as the angle from the first minimum on one side to the first minimum on the other side. Therefore, the total angular size is:
Angular Size=2θ≈2(λA)
6. Final Expression:
Thus, the angular size of the central maxima due to single slit diffraction is:
Angular Size=2λA
In single slit diffraction, light passing through a narrow slit creates a pattern of bright and dark fringes on a screen. The central maximum is the brightest part of the pattern, and it is flanked by dark minima.
The position of the first minimum in the diffraction pattern is given by the condition:
Asinθ=λ
where:
- A is the width of the slit,
- λ is the wavelength of the light,
- θ is the angle at which the first minimum occurs.
Rearranging the equation gives:
sinθ=λA
For small angles, we can use the approximation sinθ≈θ (in radians). Thus, we have:
θ≈λA
The angular size of the central maximum is defined as the angle from the first minimum on one side to the first minimum on the other side. Therefore, the total angular size is:
Angular Size=2θ≈2(λA)
Thus, the angular size of the central maxima due to single slit diffraction is:
Angular Size=2λA
Topper's Solved these Questions
Similar Questions
Knowledge Check
Angular width of central maxima of a single slit diffraction pattern is independent of
Aslit widthBfrequency of the light usedCwavelength of the light usedDdistance between slit and screenThe angular width of the central maximum of the diffraction patternn in a single slit (of width a) experiment, with λ as the wavelenth of light, is
A3λ2aBλ2aC2λaDλaIn a Young's double-slit experiment, the distance between the two identical slits is 6.1 times larger than the slit width. Then the number of intensity maxima observed within the central maximum of the single slit diffraction pattern is :
A3B6C12D24
Find the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.
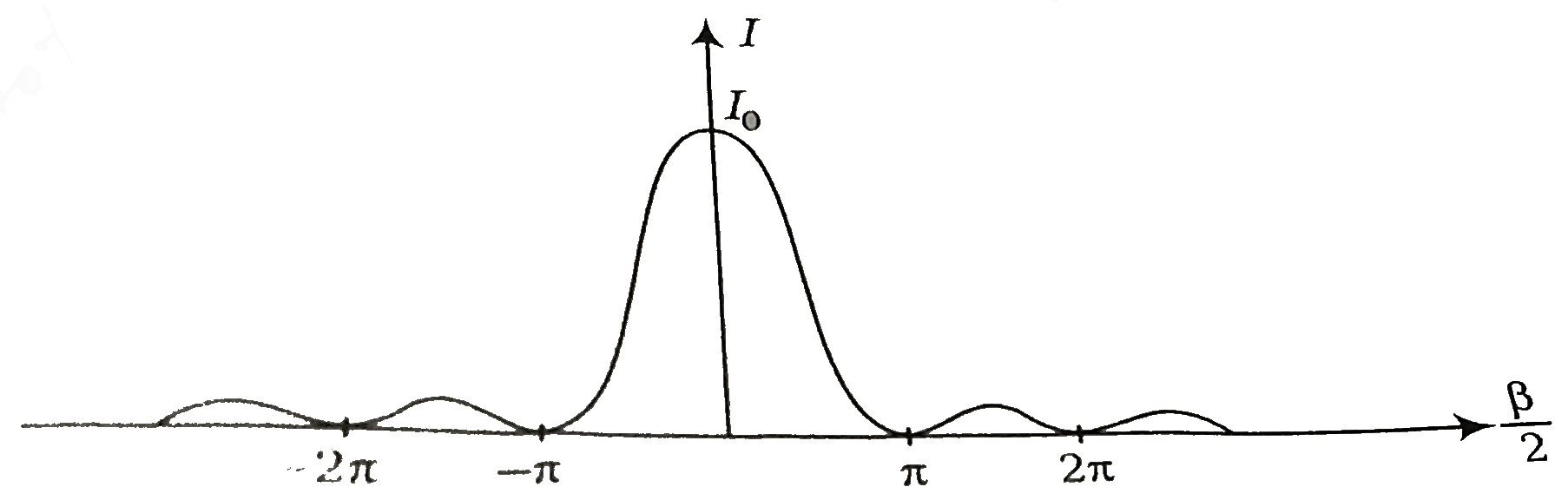
View SolutionAngular width of central maximum in diffraction at a single slit is……………. .
View SolutionLight of frequency 25 GHz is incident normally on a rectangular slit of width 4 cm. Calculate the angular width of the central maximum of the diffraction pattern formed by the slit.
View SolutionThe first diffraction minima due to a single slit diffraction is at θ=30∘ for a light of wavelength 5000Å The width of the slit is
View SolutionIn Young’s double-slit experiment, the distance between the two identical slits is 6.1 times larger than the slit width. Then the number of intensity maxima observed within the central maximum of the single-slit diffraction pattern is
View Solution

