A body of mass m= 20 g is attached to an elastic spring of length L=50 cm and spring constant k=2 Nm−1. The syste is revolved in a horizontal plan with a frequency v=30 rev/min. Find the radius of the circular motion and the tension in the spring .
0.25 m, 0.1 N
0.5 m, 0.52 N
0.55 m 0.1 N
0.9 m, 0.2 N
The correct Answer is:C
Angular velocity ω=2πr=2π×3060=πrad/s
For an elastic spring force F=kx where x is the extension.
Radius of circular motion r=L+x
Centripetal force =mrω2=F
⇒m(L+x)ω2=Kx
⇒x=mLω2k−mω2=0.02×0.5×(3.14)22−0.02×(3.14)2
≈0.05m
Radius of the circular motion (r)
=L+x=0.5+0.05
=0.55 M
Tension in the spring
T=kx=2×0.05≈0.1N
Topper's Solved these Questions
Similar Questions
A block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
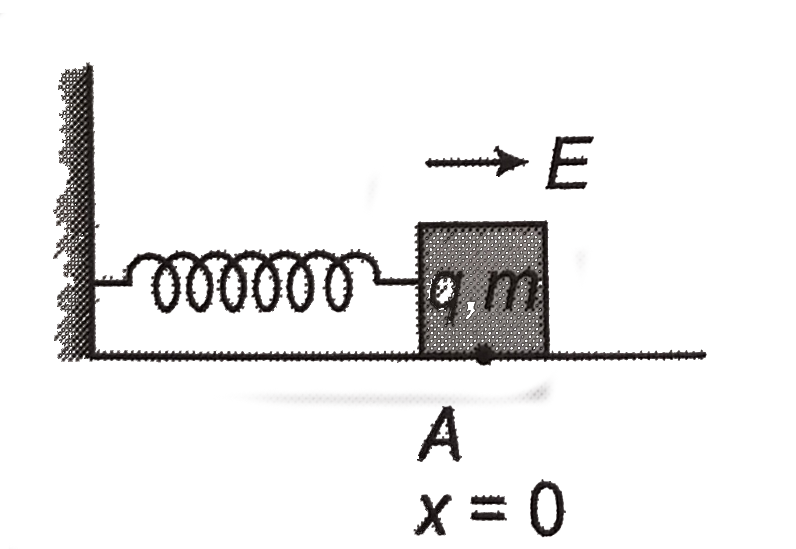
View SolutionWhen a 1.0kg mass hangs attached to a spring of length 50cm, the spring stretches by 2cm. The mass is pulled down until the length of the spring becomes 60cm. What is the amount of elastic energy stored in the spring in this condition. if g=10m/s2.
View Solution
Knowledge Check
A body of mass m= 20 g is attached to an elastic spring of length L=50 cm and spring constant k=2 Nm−1. The syste is revolved in a horizontal plan with a frequency v=30 rev/min. Find the radius of the circular motion and the tension in the spring .
A0.25 m, 0.1 NB0.5 m, 0.52 NC0.55 m 0.1 ND0.9 m, 0.2 NA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
A4×10−2B4×10−3C8×10−2D8×10−3
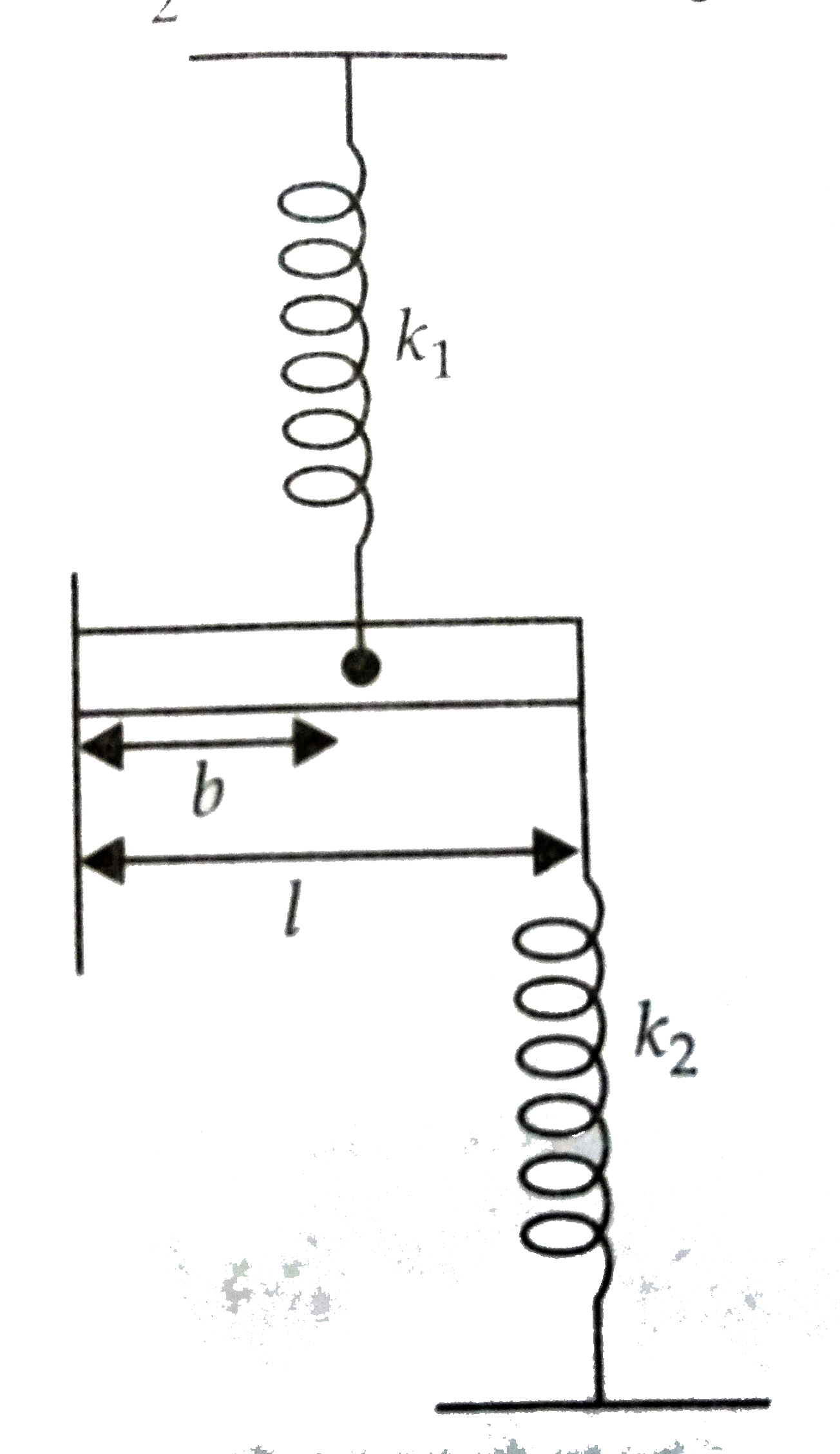
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View SolutionA block of mass 3kg is attached with an ideal spring of spring constant 900 N/m. The other end of the spring connected with a rigid wall. A fixed convex mirror of radius of curvature 120 cm is placed at a distance 110 cm from the block and the spring is in its natural length. the spring is extended by 100 cm and released. the speed of the image of block is (15n)ms, when extension in the spring remains 50 cm. Find the value of 'n'.

View SolutionA body of mass 12 kg is suspended by a coil spring of natural length 50 cm and force constant 2.0×10Nm−1. What is the stretched length of the spring ? If the body is pulled down further stretching the spring to a length of 59 cm and then released, what is the frequency of oscillation of the suspended mass ? (Neglect the mass of the spring).
View SolutionA mass m attached to spring of natural length l0 and spring constant k. One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k>>mω2 ) :
View SolutionA body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
View Solution

