In each of a set of games it is 2 to 1 in favour of the winner of the previous game. The chance that the player who wins the first game shall win three at least of the next four is
827
481
49
None of these
The correct Answer is:C
To solve the problem, we need to find the probability that the player who wins the first game will win at least three out of the next four games, given that the odds are 2 to 1 in favor of the winner of the previous game.
1. Understanding the Odds:
The odds of 2 to 1 in favor of the winner means that if the player wins, the probability of winning the next game is 23 and the probability of losing is 13.
2. Winning All Four Games:
- The probability of winning all four games is calculated as:
P(Win all 4)=(23)4=1681
3. Winning Exactly Three Games:
To find the probability of winning exactly three games, we need to consider the different scenarios in which the player can win three games and lose one. There are four different ways this can happen (the lost game can be in any of the four positions).
- Case 1: Lose the first game (LWWW)
- Probability:
P(LWWW)=13⋅(23)3=13⋅827=881
- Case 2: Lose the second game (WLWW)
- Probability:
P(WLWW)=(23)⋅13⋅(23)2=23⋅13⋅49=881
- Case 3: Lose the third game (WWLW)
- Probability:
P(WWLW)=(23)2⋅13⋅(23)=49⋅13⋅23=881
- Case 4: Lose the fourth game (WWWL)
- Probability:
P(WWWL)=(23)3⋅13=827⋅13=881
4. Total Probability of Winning Exactly Three Games:
- Adding the probabilities from all four cases:
P(Win exactly 3)=881+881+881+881=3281
5. Total Probability of Winning at Least Three Games:
- Now, we add the probability of winning all four games to the probability of winning exactly three games:
P(At least 3)=P(Win all 4)+P(Win exactly 3)=1681+3281=4881
6. Simplifying the Probability:
- Simplifying 4881:
4881=1627
Final Answer:
The probability that the player who wins the first game will win at least three out of the next four games is 1627.
The odds of 2 to 1 in favor of the winner means that if the player wins, the probability of winning the next game is 23 and the probability of losing is 13.
- The probability of winning all four games is calculated as:
P(Win all 4)=(23)4=1681
To find the probability of winning exactly three games, we need to consider the different scenarios in which the player can win three games and lose one. There are four different ways this can happen (the lost game can be in any of the four positions).
- Probability:
P(LWWW)=13⋅(23)3=13⋅827=881
- Probability:
P(WLWW)=(23)⋅13⋅(23)2=23⋅13⋅49=881
- Probability:
P(WWLW)=(23)2⋅13⋅(23)=49⋅13⋅23=881
- Probability:
P(WWWL)=(23)3⋅13=827⋅13=881
- Adding the probabilities from all four cases:
P(Win exactly 3)=881+881+881+881=3281
- Now, we add the probability of winning all four games to the probability of winning exactly three games:
P(At least 3)=P(Win all 4)+P(Win exactly 3)=1681+3281=4881
- Simplifying 4881:
4881=1627
The probability that the player who wins the first game will win at least three out of the next four games is 1627.
Topper's Solved these Questions
- PROBABILITYBook:DISHA PUBLICATIONChapter:PROBABILITYExercise:TEST YOURSELF
Explore 15 Videos
- PROBABILITYBook:DISHA PUBLICATIONChapter:PROBABILITYExercise:PRACTICE EXERCISE (STANDARD LEVEL)
Explore 65 Videos
- PERMUTATIONS AND COMBINATIONSBook:DISHA PUBLICATIONChapter:PERMUTATIONS AND COMBINATIONSExercise:TEST YOURSELF
Explore 15 Videos
- PROFIT, LOSS AND DISCOUNTBook:DISHA PUBLICATIONChapter:PROFIT, LOSS AND DISCOUNTExercise:Test Yourself
Explore 15 Videos
Similar Questions
In each of a set of games it is 2 to 1 in favor of the winner of the previous game: what is the chance that the player who wins the first game shall win three at least of the next four.
View SolutionIn a set of five games in tennis between two players A and B, the probability of a player wimxing a game is 23 who has won the earlier game. A wins the first game. What is the probability that A will win at least three of the next four games?
View Solution
Knowledge Check
The odds in favour of A winning a game of chess against B are 5:2. if three games are to be played, then the odds in favour of A's winning at least one game are 355:8 .If this is true give answer 1 else 0.
A1B0CbothDnoneTibu and Babu are playing a game in which both the players roll a pair of dice. Tibu wins if the sum of the numbers appearing on the dice is a prime number while Babu wins if the product of the numbers appearing on the dice is prime. The chance that no one wins is (both players are allowed to win simultaneously)
A1936B12C1736D49In a class, the number of students who like only Chess, only Caroms, both the games and neither of the games are in the ratio 2:4:1:3. the number of students who like at least one of these games is 120 more than those who like neither of the games. Find the number of students in the class.
A300B240C270D360
The odds in favour of A winning a game of chess against B are 5:2. if three games are to be played, then the odds in favour of A's winning at least one game are 355:8.
View SolutionTwo players P1, and P2, are playing the final of a chase championship, which consists of a series of match Probability of P1, winning a match is 2/3 and that of P2 is 1/3. The winner will be the one who is ahead by 2 games as compared to the other player and wins at least 6 games. Now, if the player P2, wins the first four matches find the probability of P1, wining the championship.
View SolutionA bag contains a white and black nails. Two players A and B alternately draw a ball from the bag replacing the ball each time after the draw till one of them draws a white ball and wins the game.A begins the game . If the probability of A winning the game is three times that of B, then the ratio a:b is
View SolutionIn a game of chess,the chance of A's win is three times the chance of a draw.The chance B's win is two times the chance of a draw.If they agree to play 3 games, then the odds in favour of they win alternately is [....... (No match is draw)
View SolutionFollowing table shows the points of each player scored in four games
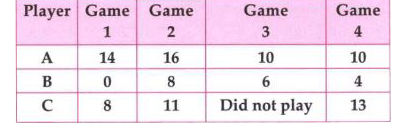
Now answer the following questions
Who is the best performer ?
View Solution