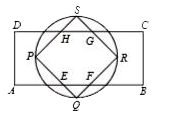
In the adjoining figure ABCD is a rectangle in which length is twice of breadth. H and G divide the line CD into three equal parts. Similarly points E and F trisect the line AB. A circle PQRS is circumscribing
a square PQRS which passes through the points E, F, G and H. What is the ratio of areas of circles to that of rectangle?
3π:7
3π:4
25π:72
32π:115
The correct Answer is:C
Step by step video, text & image solution for In the adjoining figure ABCD is a rectangle in which length is twice of breadth. H and G divide the line CD into three equal parts. Similarly points E and F trisect the line AB. A circle PQRS is circumscribing a square PQRS which passes through the points E, F, G and H. What is the ratio of areas of circles to that of rectangle? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:TEST YOURSELF
Explore 15 Videos
- MENSURATIONBook:DISHA PUBLICATIONChapter:MENSURATIONExercise:Practice Exercises (STANDARD LEVEL)
Explore 63 Videos
- LOGARITHMSBook:DISHA PUBLICATIONChapter:LOGARITHMSExercise:Test Yourself
Explore 15 Videos
- MOCK TEST - 3Book:DISHA PUBLICATIONChapter:MOCK TEST - 3Exercise:Multiple Choice Questions
Explore 20 Videos
Similar Questions
Knowledge Check
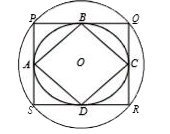
The figure shows two concentric circles with centre O. PQRS is a square inscribed in the outer circle. It also circumscribes the inner circle, touching it at point B, C, D and A. What is the ratio of the perimeter of the outer circle to that of polygon ABCD ?
 Aπ4B3π2Cπ2Dπ
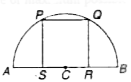
Aπ4B3π2Cπ2DπIn the adjoining figure PQRS is a square of maximum possible area which is circumscribed by the semicricle . Points R and S lie on the diameter AB. What is the area of the square if the radius of the circle is 'r' ?
 A√34r2B45r2C35r2D√54r2
A√34r2B45r2C35r2D√54r2In a triangle ABC, median AD is drawn and this median is divided into 4 equal parts by point E, F, and G such that AE = EF = FG = GD. What will be the ratio of area of ΔBFG to the area of ΔABC?
A1:12B1:15C1:8D1:6
What is the number of circles which pass through three given points not in a straight line
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
View SolutionA is a point on the circumference of a circle. Chords ABandAC divide the area of the circle into three equal parts. Find an f(x) such that angle BAC is the root of the equation, f(x)=0.
View SolutionABC is a triangle in which D, E and F are the mid-points of the sides AC, BC and AB respectively. What is the ratio of the area of the shaded to the unshaded region in the triangle?
View SolutionIn the figure given below, ABCD is a square of side 14 cm with E,F,G and H as the mid points of sides. The area of EFGH is :
View Solution