There are two disjoint sets and where
such that forms the set of natural numbers.
Also & g(a) and f(n)=g(g(n))+1 then what is g (1) ?
0
1
2
can't be determined
The correct Answer is:B
To solve the problem step by step, we need to analyze the given information about the sets S1 and S2, the functions f(n) and g(n), and their relationships.
Step 1: Understand the Sets and Functions
We have two disjoint sets:
- S1={f(1),f(2),f(3),…}
- S2={g(1),g(2),g(3),…}
It is given that S1∪S2 forms the set of natural numbers N. This means every natural number is either in S1 or S2, but not in both.
Step 2: Analyze the Properties of the Functions
We know:
- f(1)<f(2)<f(3)<… (increasing)
- g(1)<g(2)<g(3)<… (increasing)
- The relationship f(n)=g(g(n))+1
Step 3: Establish Relationships
From the equation f(n)=g(g(n))+1, we can deduce that:
- f(n)>g(g(n)) because g(g(n))+1 is always greater than g(g(n)).
Step 4: Compare f(n) and g(n)
Since f(n)>g(g(n)) and g(n) is increasing, we can conclude:
- f(n)>g(n) for all n.
Step 5: Determine the Smallest Element
Since S1 and S2 are disjoint and together they cover all natural numbers, the smallest element in S1∪S2 must be 1 (the smallest natural number).
Step 6: Identify g(1)
Since g(1) is the smallest element in S2 and S2 must contain natural numbers that are not in S1, we can conclude:
- The smallest number in S2 (which is g(1)) must be 1, because if g(1) were 0 or any number less than 1, it would not be a natural number.
Conclusion
Thus, we conclude that:
g(1)=1
Final Answer
The value of g(1) is 1.
We have two disjoint sets:
- S1={f(1),f(2),f(3),…}
- S2={g(1),g(2),g(3),…}
We know:
- f(1)<f(2)<f(3)<… (increasing)
- g(1)<g(2)<g(3)<… (increasing)
- The relationship f(n)=g(g(n))+1
From the equation f(n)=g(g(n))+1, we can deduce that:
- f(n)>g(g(n)) because g(g(n))+1 is always greater than g(g(n)).
Since f(n)>g(g(n)) and g(n) is increasing, we can conclude:
- f(n)>g(n) for all n.
Since S1 and S2 are disjoint and together they cover all natural numbers, the smallest element in S1∪S2 must be 1 (the smallest natural number).
Since g(1) is the smallest element in S2 and S2 must contain natural numbers that are not in S1, we can conclude:
- The smallest number in S2 (which is g(1)) must be 1, because if g(1) were 0 or any number less than 1, it would not be a natural number.
Thus, we conclude that:
g(1)=1
The value of g(1) is 1.
Topper's Solved these Questions
- SET THEORYBook:DISHA PUBLICATIONChapter:SET THEORYExercise:Test Yourself
Explore 15 Videos
- SET THEORYBook:DISHA PUBLICATIONChapter:SET THEORYExercise:Practice Exercises (Standard Level)
Explore 31 Videos
- RATIO,PROPORTION AND VARIATIONBook:DISHA PUBLICATIONChapter:RATIO,PROPORTION AND VARIATIONExercise:Test Yourself
Explore 15 Videos
- TIME AND WORKBook:DISHA PUBLICATIONChapter:TIME AND WORKExercise:Test Yourself
Explore 15 Videos
Similar Questions
Knowledge Check
If f(x)=3x−1,g(x)=x2+1 then f[g(x)]=
A3x2+2B9x2−6x+2C3x2−2D9x2+6x−2If f(x) = 3x + 1 and g(x) =x2−1, then (f + g) (x) is equal to
Ax2+3xBx2−3x+2Cx2+3x+2Dx2−3xIf f={(1,2),(2,3),(3,5),(5,8)}andg={(2,1),(3,2),(5,3),(8,5)} then f∘g=
A{(1,2),(2,3),(3,5),(5,8),(2,1),(3,2),(5,3),(8,5)}B{(2,2),(3,3),(5,5),(8,8,)}C{(1,1),(2,2),(3,3),(5,5)}Dnone of these.
If f(x)=3x+1 and g(x)=x3+2 then (f+gf⋅g)(0) is:
View SolutionIf the function f(x)=x3+eπ2andg(x)=f−1(x), then the value of g '(1) = _________
View Solution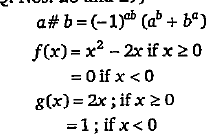
Find the value of f(g(2#3)+g(f(1#2) :
View SolutionLet f:R→R:f(x)=(2x−3) and g:R→R:g(x)=12(x+3)
show that (f o g) =IR=(gof)
View SolutionIf f(x)=12−tan(πx2),−1<x<1 and g(x)=√3+4x−4x2, then domain (f+g) is given by
View Solution