The angle of elevation and depression of top of a statue from a point 32 feet above the lake are respectively αandβ. If sinα=513andcosβ=35 then what is the height of the statue from the surface of the lake ?
44 feet
42 feet
33 feet
55 feet
The correct Answer is:D
To solve the problem step by step, we will use trigonometric relationships based on the angles of elevation and depression.
Step 1: Understand the Geometry
We have a point 32 feet above the lake from which the angles of elevation (α) and depression (β) to the top of the statue are given. We need to find the height of the statue (h) from the surface of the lake.
Step 2: Set Up the Trigonometric Relationships
From the problem, we know:
- sinα=513
- cosβ=35
Using the definitions of sine and cosine:
- For angle α (elevation):
sinα=height of statuehypotenuse⇒sinα=h√h2+322
- For angle β (depression):
cosβ=basehypotenuse⇒cosβ=32√h2+322
Step 3: Express h in terms of x and y
Let:
- For angle α, we can set h=5x and the hypotenuse as 13x.
- For angle β, we can set 32=3y and the hypotenuse as 5y.
Step 4: Find the Relationships
From the triangle formed by the angle α:
√h2+322=13x
Substituting h=5x:
√(5x)2+322=13x
Squaring both sides:
25x2+1024=169x2
Rearranging gives:
144x2=1024⇒x2=1024144=649⇒x=83
Step 5: Calculate h
Now substituting back for h:
h=5x=5×83=403 feet
Step 6: Find y
From the triangle formed by angle β:
√h2+322=5y
Substituting h=403:
√(403)2+322=5y
Squaring both sides:
16009+1024=25y2
Converting 1024 to a fraction with a denominator of 9:
1600+92169=25y2⇒108169=25y2
Thus:
y2=10816225⇒y=10415
Final Answer
The height of the statue from the surface of the lake is:
h=403 feet≈13.33 feet
We have a point 32 feet above the lake from which the angles of elevation (α) and depression (β) to the top of the statue are given. We need to find the height of the statue (h) from the surface of the lake.
From the problem, we know:
- sinα=513
- cosβ=35
- For angle α (elevation):
sinα=height of statuehypotenuse⇒sinα=h√h2+322
- For angle β (depression):
cosβ=basehypotenuse⇒cosβ=32√h2+322
Let:
- For angle α, we can set h=5x and the hypotenuse as 13x.
- For angle β, we can set 32=3y and the hypotenuse as 5y.
From the triangle formed by the angle α:
√h2+322=13x
Substituting h=5x:
√(5x)2+322=13x
Squaring both sides:
25x2+1024=169x2
Rearranging gives:
144x2=1024⇒x2=1024144=649⇒x=83
Now substituting back for h:
h=5x=5×83=403 feet
From the triangle formed by angle β:
√h2+322=5y
Substituting h=403:
√(403)2+322=5y
Squaring both sides:
16009+1024=25y2
Converting 1024 to a fraction with a denominator of 9:
1600+92169=25y2⇒108169=25y2
Thus:
y2=10816225⇒y=10415
The height of the statue from the surface of the lake is:
h=403 feet≈13.33 feet
Topper's Solved these Questions
- HEIGHT AND DISTANCEBook:LUCENT PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:EXERCISE-12B
Explore 14 Videos
- HEIGHT AND DISTANCEBook:LUCENT PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:EXERCISE-12B
Explore 14 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
- INDICES AND SURDS Book:LUCENT PUBLICATIONChapter:INDICES AND SURDS Exercise:Exercise - 2B
Explore 14 Videos
Similar Questions
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be αandβ respectively. Prove that the height of the house is h(1+tanα⋅tanβ) metres.
View SolutionIf sinα=13andcosβ=45, then find sin(α+β).
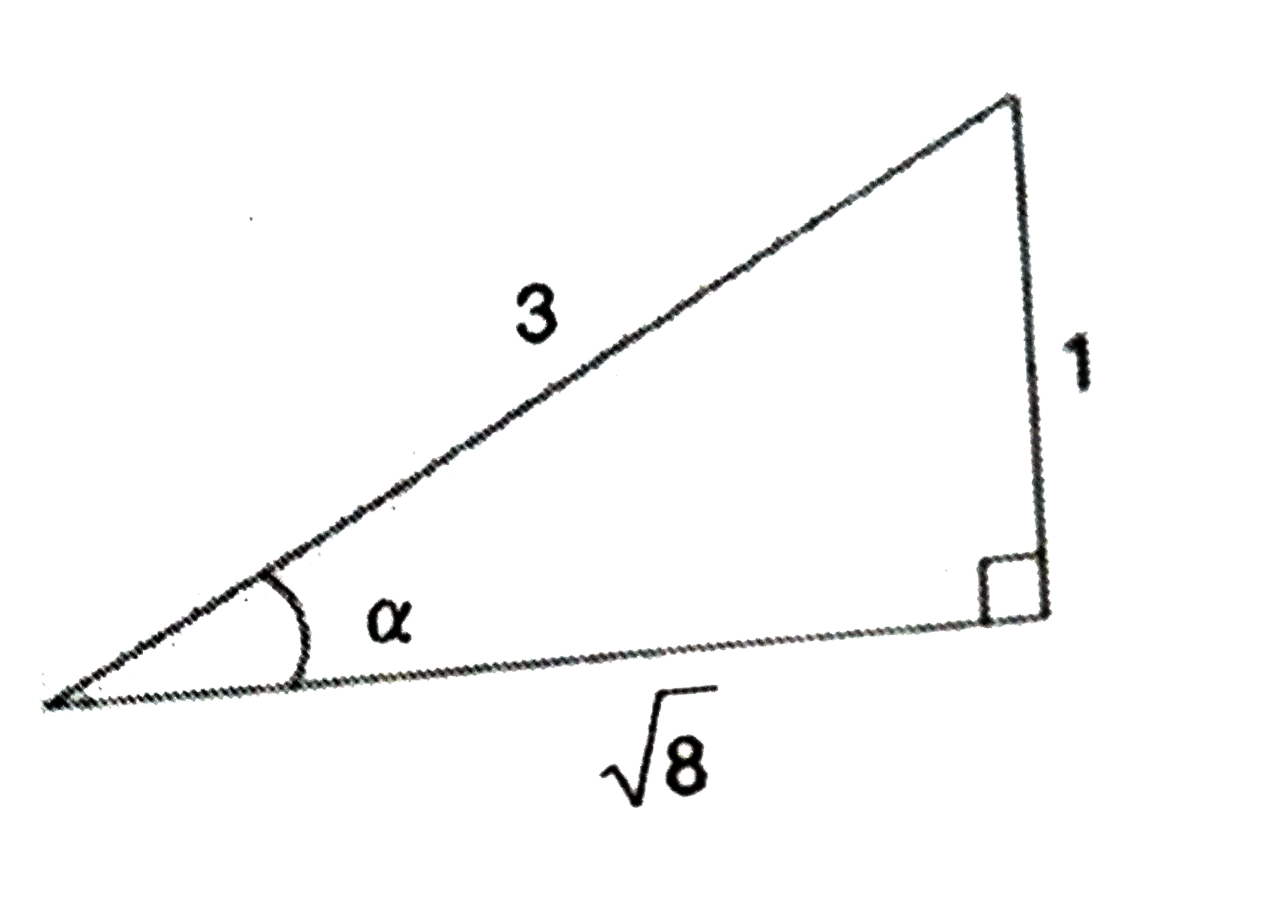
View Solution
Knowledge Check
The angles of elevation of a pole from two points which are 75 m and 48 m away from its base are α and β respectively. If α and β are complementary, then the height of the tower is:
A54.5 mB61.5 mC60 mD50 mThe angle of elevation of a cloud from a height h above the level of water in a lake is α and the angle of depressionof its image in the lake is β. Find the height of the cloud above the surface of the lake:
Ahsin(β−α)sin(α+β)BhsinαChsin(α+β)sin(β−α)Dnone of theseFrom the top of a building, the angle of elevation and depression of top and bottom of a tower are 60∘and30∘ respectively. If the height of the building is 5 m, then find the height of the tower.
A10√3mB15 mC15√3mD20 m
The angle of elevation of an aeroplane from a point 200m above a lake surface is 45∘ and the angle of depression of its reflection is 75∘ .The height of the aeroplane above the surface of the lake is
View SolutionIf the angle of elevation of a cloud from a point 10 metres above a lake is 30∘ and the angle of depression of its reflection in the lake is 60∘. Find the height of the cloud from the surface of lake.
View SolutionA marble statue of height h1 metres is mounted on a pedestal. The angles of elevation of the top and bottom of the statue from a point h2 metres above the ground level are αandβ respectively. Show that the height of the pedestal is (h1−h2)tanβ+h2tanαtanα−tanβ.
View SolutionThe angle of elevation of a stationary cloud from a point 2500 feet above a lake is 30∘ and the angle of depression of its reflection in the lake is 45∘.Find the height of cloud above the lake water surface .
View SolutionThe angle of elevation of the top of a tower from a point 20 m away from its base is 45∘.What is the height of the tower?
View Solution
