A cow is tied in a pole with a rope. The cow moves in a circular pan keeping rope straight. When it covers a distance of 44 meter an angle of 72° is subtended at the centre. The length of the rope is:
45 m
35 m
22 m
56 m
The correct Answer is:B
To find the length of the rope, we can use the relationship between the arc length, the radius of the circular path, and the angle subtended at the center. The formula for the arc length L is given by:
L=θ360∘×2πr
Where:
- L is the arc length,
- θ is the angle in degrees,
- r is the radius (length of the rope).
Given:
- L=44 meters,
- θ=72∘.
We need to find the radius r.
Step 1: Substitute the known values into the formula
44=72360×2πr
Step 2: Simplify the fraction
72360=15(since 72÷72=1 and 360÷72=5)
Now the equation becomes:
44=15×2πr
Step 3: Multiply both sides by 5 to eliminate the fraction
44×5=2πr
220=2πr
Step 4: Divide both sides by 2π
r=2202π
Step 5: Substitute π with 227
r=2202×227=220×744
Step 6: Simplify the expression
r=154044=35 meters
Thus, the length of the rope is 35 meters.
Final Answer:
The length of the rope is 35 meters.
---
- L is the arc length,
- θ is the angle in degrees,
- r is the radius (length of the rope).
- L=44 meters,
- θ=72∘.
The length of the rope is 35 meters.
Topper's Solved these Questions
- ELEMENTARY TRIGONOMETRIC IDENTITIES Book:LUCENT PUBLICATIONChapter:ELEMENTARY TRIGONOMETRIC IDENTITIES Exercise:EXERCISE 11B
Explore 37 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES Book:LUCENT PUBLICATIONChapter:ELEMENTARY TRIGONOMETRIC IDENTITIES Exercise:EXERCISE 11B
Explore 37 Videos
- CONGRUENCE AND SIMILAR TRIANGLES Book:LUCENT PUBLICATIONChapter:CONGRUENCE AND SIMILAR TRIANGLES Exercise:EXERCISE-5B
Explore 8 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
Similar Questions
A horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight, and describes 88 metres when it traces 72∘ at the centre, find the length of the rope.
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of 12∘ with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View Solution
Knowledge Check
A horse is tied to a post by a rop. If the horse moves along a circular path always keeping the rope stretched and describes 88 metres when it as traced out 72∘ at the centre, the length of the rope is
(take π=227)A70 mB75 mC80 mD65 mA horse is tied to a post by a rop. If the horse moves along a circular path always keeping the rope stretched and describes 88 metres when it as traced out 72∘ at the centre, the length of the rope is
(take π=227)A70 मीटरB75 मीटरC80 मीटरD65 मीटरA horse is tied to a post by a rop. If the horse moves along a circular path always keeping the rope stretched and describes 88 metres when it as traced out 72∘ at the centre, the length of the rope is
(take π=227)A40 mB32 mC70 mD88 m
A 40-kg mass hanging at the end of a rope of length l. Oscillates in a vertical plane with an angular of θ0. What is the tension in the rope when it makes an angle θ with the vertial ? If the breaking strength of the rope is 80 kg, what is the maximum angular amplitude with which the mass can oscillate without the rope breaking ?
View SolutionA 40 kg mass, hanging at the end fo a rope of length l, oscillates in a vertical plane with an angular amplitude θ0. What is the tension in the rope when it makes en angle θ with the vertical ? If the breaking strength of the rope is 80kg, what is the maximum amplitude with which the mass can oscillate without the rope breaking?
View SolutionRohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A which is are a distance of 30m from D such the ∠DC=900
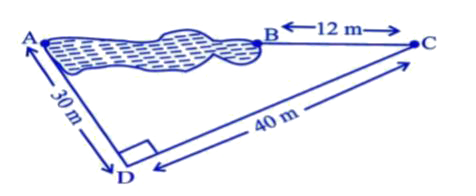
Find the length of the rope used.
View SolutionThe tops of two poles of heights 18 metresand 12 metres are connected by a rope. irthe rope makes an angle 30∘ with thehorizontal, the length of the rope in metres is
View SolutionAn ant moves along a circular track of 6 m radius such that the arc of the circular track subtends an angle of 30∘ at the centre. The distance covered by the ant is
View Solution
