Which of the folowing pair represent equation of parallel straight lines.
2x+3y=4,4x+6y=9
x+2y=4,2x+y=4
y=3x+5,x=3y+5
None of these
The correct Answer is:C
To determine which pair of equations represents parallel straight lines, we will use the condition for parallel lines in the form of linear equations. The condition states that for two lines represented by the equations A1x+B1y=C1 and A2x+B2y=C2, the lines are parallel if:
A1A2=B1B2≠C1C2
Now, let's analyze each option step-by-step.
Step 1: Analyze the First Option
The first option is:
1. 2x+3y=4 (Equation 1)
2. 4x+6y=9 (Equation 2)
Identify coefficients:
- For Equation 1: A1=2, B1=3, C1=4
- For Equation 2: A2=4, B2=6, C2=9
Calculate ratios:
- A1A2=24=12
- B1B2=36=12
- C1C2=49
Check conditions:
- Since A1A2=B1B2 and C1C2≠12, the first option satisfies the condition for parallel lines.
Step 2: Analyze the Second Option
The second option is:
1. x+2y=4 (Equation 1)
2. 2x+y=4 (Equation 2)
Identify coefficients:
- For Equation 1: A1=1, B1=2, C1=4
- For Equation 2: A2=2, B2=1, C2=4
Calculate ratios:
- A1A2=12
- B1B2=21=2
Check conditions:
- Since A1A2≠B1B2, the second option does not satisfy the condition for parallel lines.
Step 3: Analyze the Third Option
The third option is:
1. y=3x+5 (Equation 1)
2. x=3y+5 (Equation 2)
Rearranging Equation 2:
- Rearranging x=3y+5 gives us −3y+x=5 or x−3y=5.
Identify coefficients:
- For Equation 1: A1=−3, B1=1, C1=5
- For Equation 2: A2=1, B2=−3, C2=5
Calculate ratios:
- A1A2=−31=−3
- B1B2=1−3
Check conditions:
- Since A1A2≠B1B2, the third option does not satisfy the condition for parallel lines.
Final Conclusion
Only the first option satisfies the condition for parallel lines. Therefore, the answer is:
Answer: The first option 2x+3y=4 and 4x+6y=9 represents parallel straight lines.
---
The first option is:
1. 2x+3y=4 (Equation 1)
2. 4x+6y=9 (Equation 2)
- For Equation 1: A1=2, B1=3, C1=4
- For Equation 2: A2=4, B2=6, C2=9
- A1A2=24=12
- B1B2=36=12
- C1C2=49
- Since A1A2=B1B2 and C1C2≠12, the first option satisfies the condition for parallel lines.
The second option is:
1. x+2y=4 (Equation 1)
2. 2x+y=4 (Equation 2)
- For Equation 1: A1=1, B1=2, C1=4
- For Equation 2: A2=2, B2=1, C2=4
- A1A2=12
- B1B2=21=2
- Since A1A2≠B1B2, the second option does not satisfy the condition for parallel lines.
The third option is:
1. y=3x+5 (Equation 1)
2. x=3y+5 (Equation 2)
- Rearranging x=3y+5 gives us −3y+x=5 or x−3y=5.
- For Equation 1: A1=−3, B1=1, C1=5
- For Equation 2: A2=1, B2=−3, C2=5
- A1A2=−31=−3
- B1B2=1−3
- Since A1A2≠B1B2, the third option does not satisfy the condition for parallel lines.
Only the first option satisfies the condition for parallel lines. Therefore, the answer is:
Topper's Solved these Questions
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES Book:LUCENT PUBLICATIONChapter:ELEMENTARY TRIGONOMETRIC IDENTITIES Exercise:EXERCISE 11B
Explore 37 Videos
- HEIGHT AND DISTANCEBook:LUCENT PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:EXERCISE-12B
Explore 14 Videos
Similar Questions
Knowledge Check
Which of the folowing represent Z or trans?
A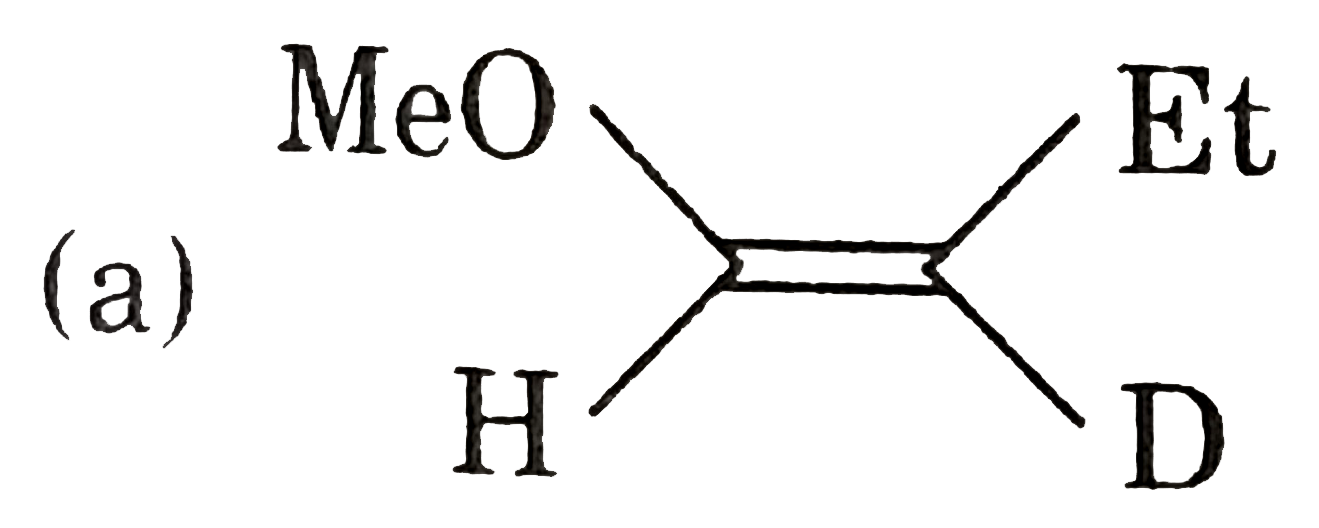 B
B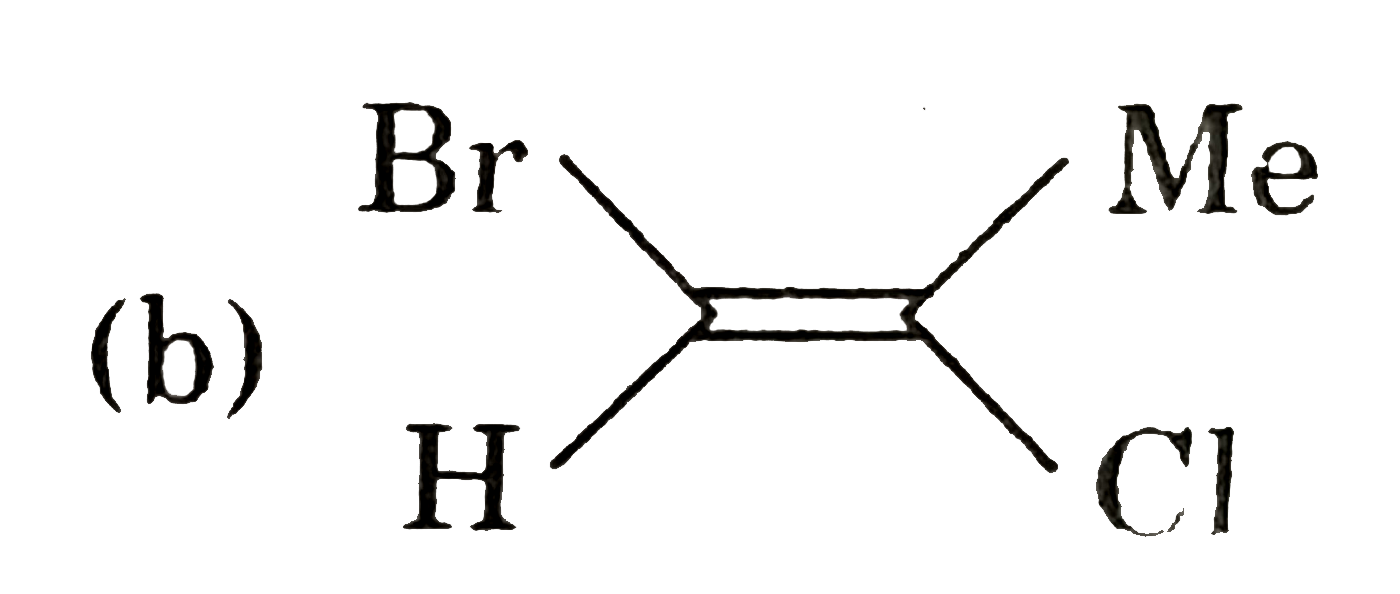 C
C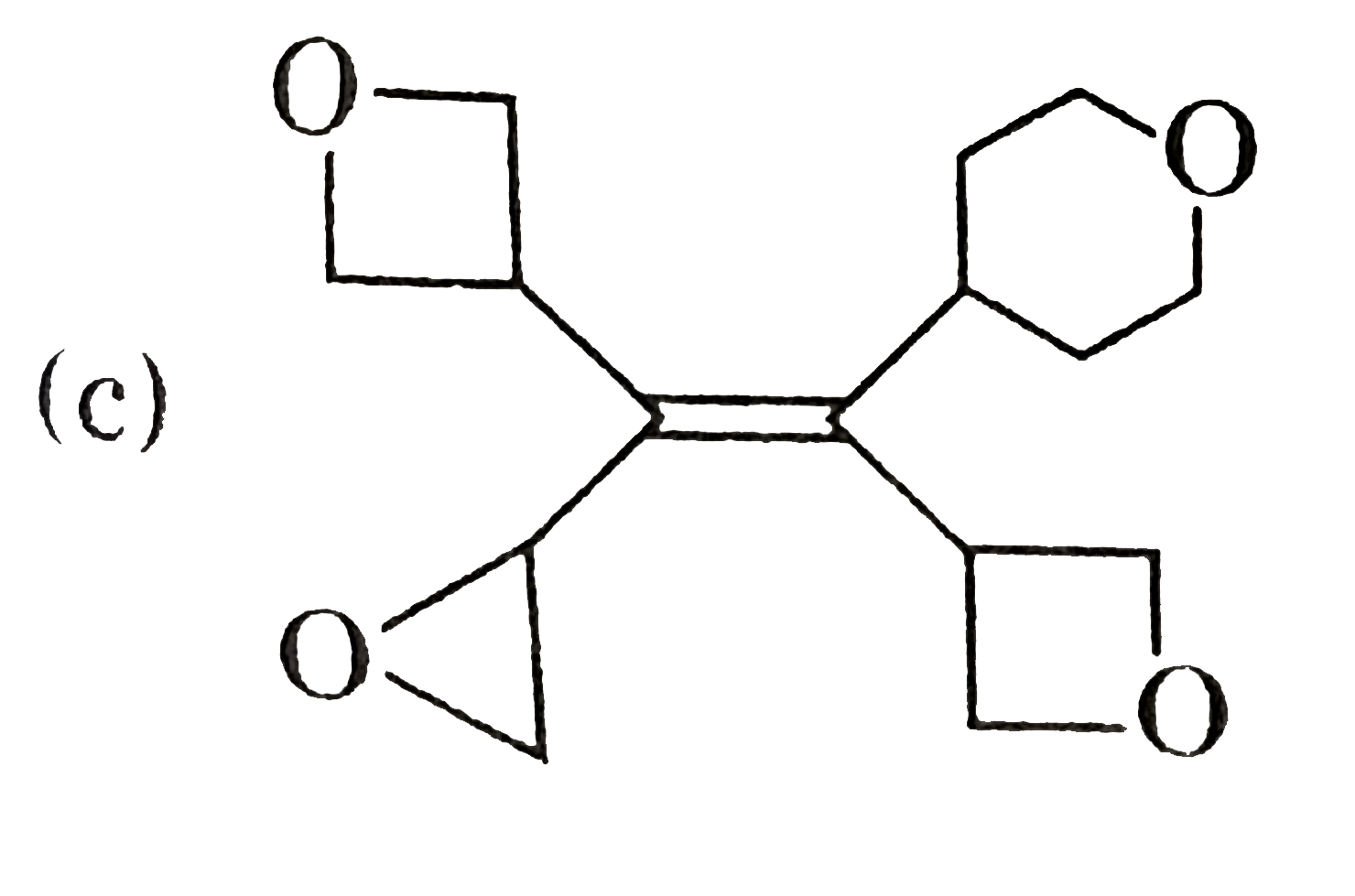 D
D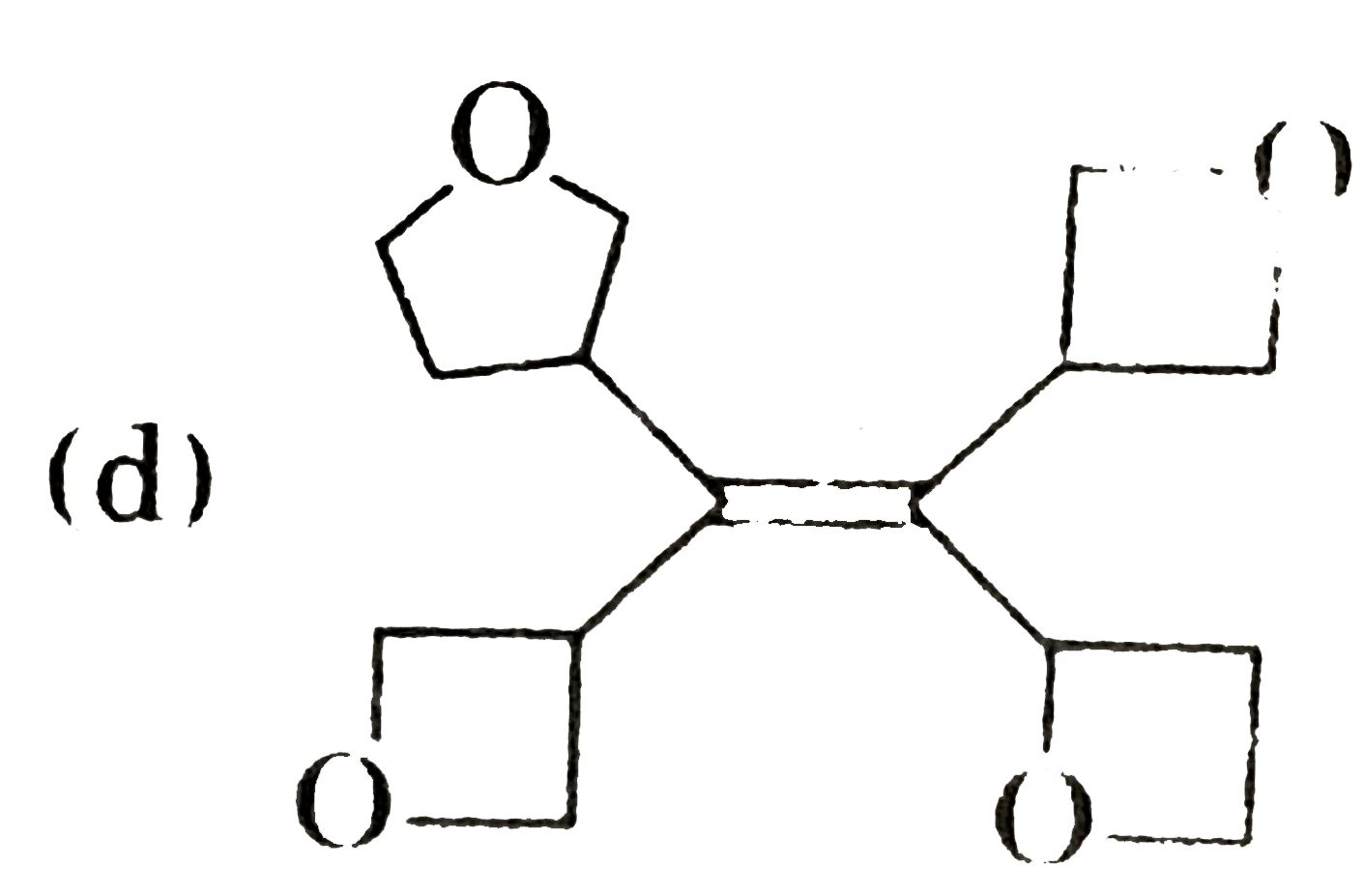
Which of the following represents pair of lines?
A2x2+3xy−2y2+5x+5y+3=0B2x2−2y2+5x+5y+3=0C2x2+5xy−2y2+5x+5y+3=0D2x2+3xy−4y2+5x+5y+3=0Which of the following equation represents a line parallel to y axis
A2x=3yB2y=4C2x=4D2x-3y=9
Which of the following equations represents a line parallel to x axis
View SolutionWhich of the following will be the equation of a straight line parallel to the y-axis at a distance of 9 units to the left?
View SolutionWhich of the folowing represents hydrolysis ? .
View SolutionWhich of the following equations represents a pair of real and coincident straight lines?
View SolutionWhich of the following equation does not represent a pair of lines ?
View Solution
