Straight line 2x+3y+10=0 inersects coordinate axes respectively are the points
(−5,0)(0,−103)
(103,0)(0,5)
(−5,0),(0,103)
(−103,0),(0,−53)
The correct Answer is:A
To find the points where the straight line 2x+3y+10=0 intersects the coordinate axes, we need to determine the x-intercept and y-intercept of the line.
Step 1: Find the x-intercept
The x-intercept occurs where y=0. We substitute y=0 into the equation of the line:
2x+3(0)+10=0
This simplifies to:
2x+10=0
Now, we solve for x:
2x=−10
x=−5
Thus, the x-intercept is the point Q(−5,0).
Step 2: Find the y-intercept
The y-intercept occurs where x=0. We substitute x=0 into the equation of the line:
2(0)+3y+10=0
This simplifies to:
3y+10=0
Now, we solve for y:
3y=−10
y=−103
Thus, the y-intercept is the point P(0,−103).
Final Result
The points where the line intersects the coordinate axes are:
- x-intercept: Q(−5,0)
- y-intercept: P(0,−103)
The x-intercept occurs where y=0. We substitute y=0 into the equation of the line:
x=−5
The y-intercept occurs where x=0. We substitute x=0 into the equation of the line:
y=−103
The points where the line intersects the coordinate axes are:
- x-intercept: Q(−5,0)
- y-intercept: P(0,−103)
Topper's Solved these Questions
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION Book:LUCENT PUBLICATIONChapter:GRAPHICAL SOLUTION OF LINEAR EQUATION Exercise:EXERCISE-3B
Explore 8 Videos
- ELEMENTARY TRIGONOMETRIC IDENTITIES Book:LUCENT PUBLICATIONChapter:ELEMENTARY TRIGONOMETRIC IDENTITIES Exercise:EXERCISE 11B
Explore 37 Videos
- HEIGHT AND DISTANCEBook:LUCENT PUBLICATIONChapter:HEIGHT AND DISTANCEExercise:EXERCISE-12B
Explore 14 Videos
Similar Questions
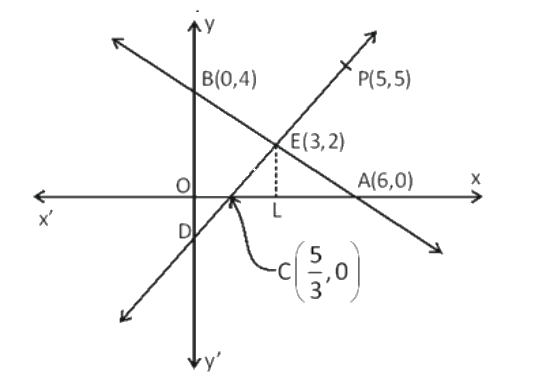
The line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionIf the lines 2x+3y−1=0andkx−y+4=0 intersect the coordinate axes in concyclic points then k−1=
View Solution
Knowledge Check
Area of triangle between the straight line 2x+2y−6=0 and coordinate axes is ... Square unit.
A3B32C6D92A point on the straight line, 3x+5y=15 which is equidistant from the coordinate axes will lie only in
AIV quadrantBI quadrantCI and II quadrantDI , II and IV quadrantConsider the parabola y=x2+7x+2 and the straight line y = 3x -3.
What are the coordinates of the point on the parabola which is closest to the straight line?A(0, 2)B(-2, -8)C(-7, 2)D(1, 10)
A straight line 4x+3y=72 intersect the x and y axes at A and B respectively. Then Distance between the incentre and the orthocentre of the triangle AOB is
View SolutionA line passes through (−3,4) and the portion of the line intercepted between the coordinate axes is bisected at the point then equation of line is (A) 4x−3y+24=0 (B) x−y−7=0 (C) 3x−4y+25=0 (D) 3x−4y+24=0
View SolutionThe lines 2x+3y+19=0 and 9x+6y−17=0 , cut the coordinate axes at concyclic points.
View SolutionFind the transformed equation of the straight line 2x−3y+5=0, when the origin is shifted to the point (3,−1) after translation of axes.
View SolutionThe area of the triangle formed by the straight line 2x−3y+6=0 with the co-ordinate axes is (in sq.units)
View Solution
