The diameter of two hollow sphere made from the same metal sheet are 21 cm and 17.5 cm respectively. The ratio of the area of metal sheets required for making the two sphere is
6:5
36:25
3:2
18:25
The correct Answer is:B
To find the ratio of the area of metal sheets required for making the two hollow spheres, we need to calculate the surface area of each sphere and then find the ratio of these areas.
Step 1: Find the radius of each sphere.
- The diameter of the first sphere is 21 cm, so the radius r1 is:
r1=212=10.5 cm
- The diameter of the second sphere is 17.5 cm, so the radius r2 is:
r2=17.52=8.75 cm
Step 2: Calculate the surface area of each sphere.
The formula for the surface area A of a sphere is given by:
A=4πr2
- For the first sphere:
A1=4π(10.5)2=4π×110.25=441π cm2
- For the second sphere:
A2=4π(8.75)2=4π×76.5625=306.25π cm2
Step 3: Find the ratio of the surface areas.
To find the ratio of the areas A1 and A2:
Ratio=A1A2=441π306.25π=441306.25
To simplify this ratio, we can multiply both the numerator and the denominator by 100 to eliminate the decimal:
4410030625
Now, we can simplify this fraction. Dividing both by 25:
17641225
Now, we can further simplify this ratio:
1764÷17641225÷1764=10.693
This gives us a ratio of approximately:
441306.25≈17641225
Final Step: Write the final ratio.
The ratio of the area of metal sheets required for making the two spheres is:
441306.25≈17641225
- The diameter of the first sphere is 21 cm, so the radius r1 is:
r1=212=10.5 cm
- The diameter of the second sphere is 17.5 cm, so the radius r2 is:
r2=17.52=8.75 cm
The formula for the surface area A of a sphere is given by:
A=4πr2
- For the first sphere:
A1=4π(10.5)2=4π×110.25=441π cm2
- For the second sphere:
A2=4π(8.75)2=4π×76.5625=306.25π cm2
To find the ratio of the areas A1 and A2:
Ratio=A1A2=441π306.25π=441306.25
To simplify this ratio, we can multiply both the numerator and the denominator by 100 to eliminate the decimal:
4410030625
Now, we can simplify this fraction. Dividing both by 25:
17641225
Now, we can further simplify this ratio:
1764÷17641225÷1764=10.693
This gives us a ratio of approximately:
441306.25≈17641225
The ratio of the area of metal sheets required for making the two spheres is:
441306.25≈17641225
Topper's Solved these Questions
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - V
Explore 304 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE VI
Explore 47 Videos
- MENSURATIONBook:KIRAN PUBLICATIONChapter:MENSURATIONExercise:TYPE - III
Explore 21 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
- MISCELLANEOUSBook:KIRAN PUBLICATIONChapter:MISCELLANEOUSExercise:TYPE-VI
Explore 15 Videos
Similar Questions
The diameter and thickness of a hollow metal sphere are 12 cm and 0.01 m respectively. The density of the metal is 8.88 gm per cm2. Find the outer surface area and mass of the sphere. [π=3.14]
View SolutionThe diameter and thickkness of a hollow metals sphere are 12 cm and 0.01 m respectively. They density of the metal is 8.88 gm per cm^3.
Find the outer surface area and mass of the sphere.
Given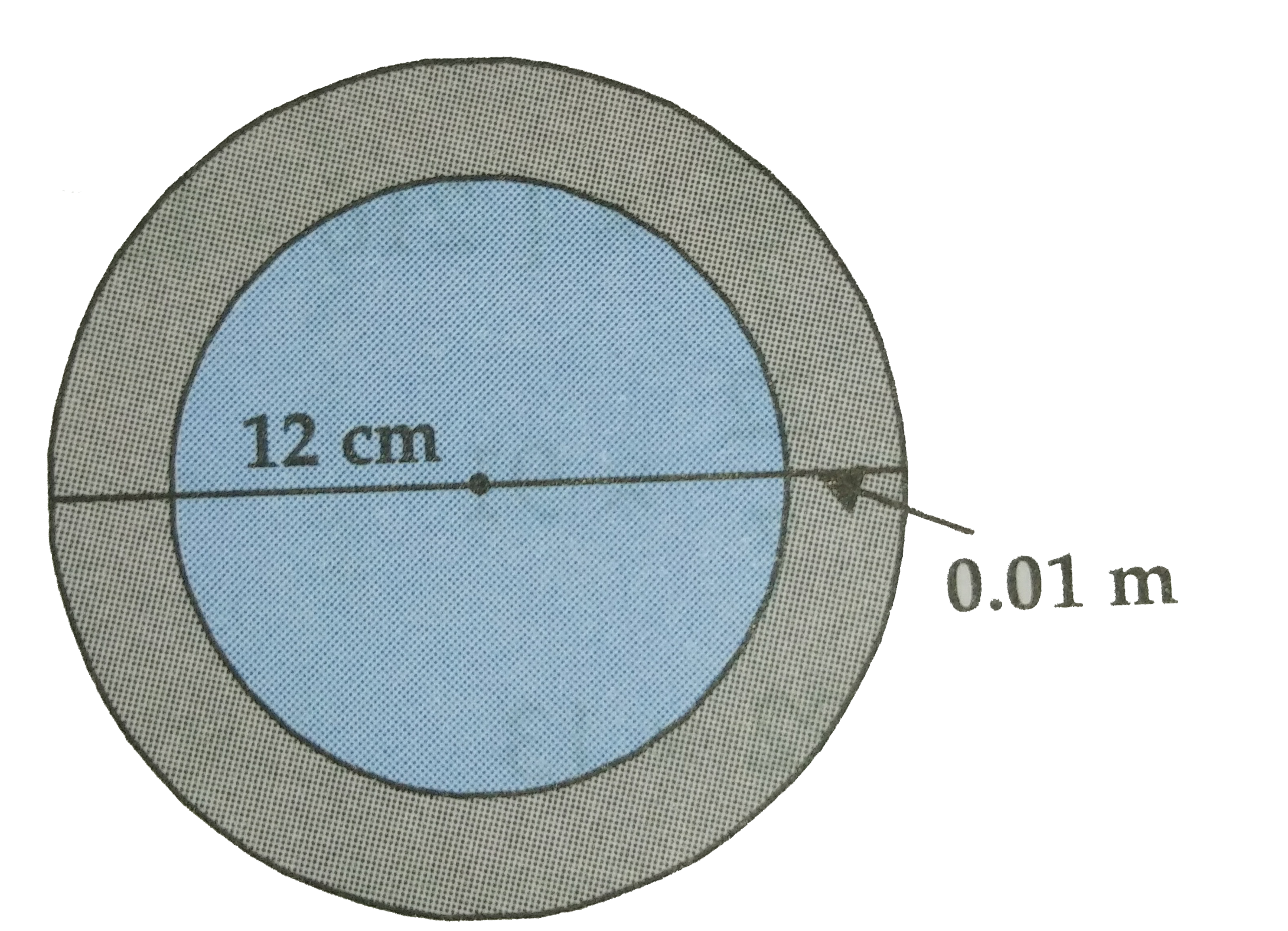
For hollow metal sphere
Outer radiu =r2=Diameter2
=122=6cm
Thickness =x=0.01m=0.01×100cm
Thickness =x=1cm
Inner radius =r1=r2−x
Density =8.88gmpercm3
To find (i) Outer surface area
(ii) Mass of sphere
View Solution
Knowledge Check
Metallic spheres of radii 7 cm, 9 cm and 11 cm respectively are melted to form a single solid sphere. The radius of the resulting sphere is
A10 cmB8.6 cmC11.5 cmD13.39 cmTwo solid spheres are made of the same material. The ratio of their diameters is 2: 1. The ratio of their moments of inertia about their respective diameters is
A1:4B8:1C32:1D16:1Two isolated metallic spheres of radii 2 cm and 4 cm are given equal charge, then the ratio of charge density on the surfaces of the spheres will be
A1:2B4:1C8:1D1:4
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1 m3 of metal weighs 21 g.
View SolutionA bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of Rs 10 per 100cm2 .
View SolutionThe base diameter and height of a metallic cone are 24cm and 6cm respectively .It is melted and recast in to a sphere.Find the surface area of the sphere.
View SolutionThe diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10cm and 30cm respectively.If its height is 24cm ,find : (i) The area of the metal sheet used to make the bucket.
View SolutionMetallic spheres of radii 6cm, 8cm and 10cm respectively are melted to form a solid sphere. Find the radius of the resulting sphere.
View Solution
