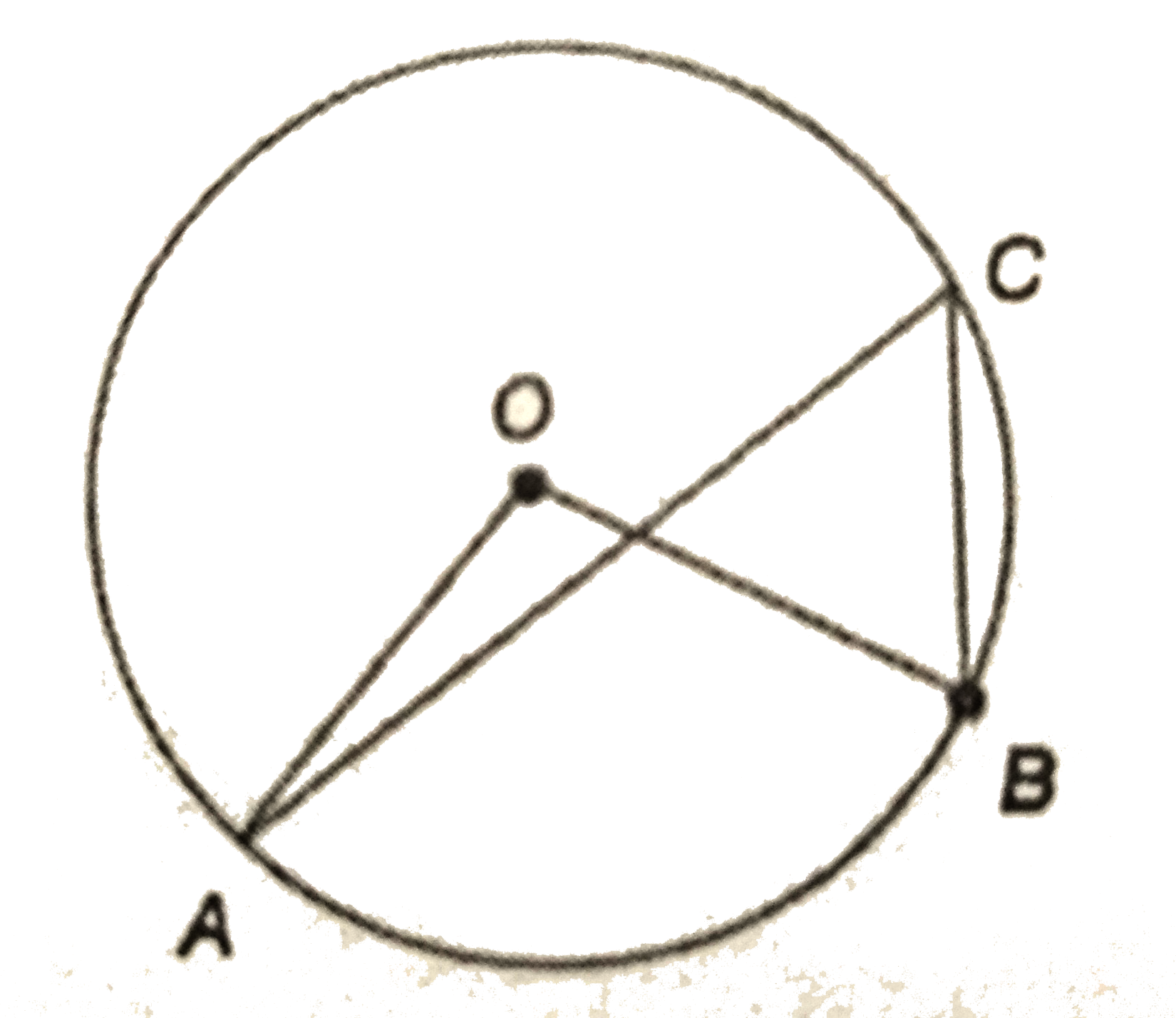The two banks of a canal are straight and parallel .A,B,C are three persons of whom A stands on one bank and B and C on the opposite banks ,B finds the angle ABC is 30∘,while C finds that the angle ACB 60∘ .If B and C are 100 metres apart ,the breadth of the canal is
25√3 metres
20√3 metres
25√3 metres
20√3 metres
The correct Answer is:C
To solve the problem, we will use the properties of triangles and trigonometric ratios. Here's a step-by-step solution:
Step 1: Understand the Setup
We have a canal with two banks that are parallel. Points A, B, and C represent three persons, where A is on one bank and B and C are on the opposite bank. The angles given are:
- Angle ABC = 30°
- Angle ACB = 60°
Step 2: Identify the Triangle
From the information given, we can form triangle ABC. The sides of the triangle are:
- BC = 100 meters (the distance between B and C)
- We need to find the height (the breadth of the canal), which is the perpendicular distance from point A to line BC.
Step 3: Use the Angles to Find the Height
In triangle ABC:
- The angle at B (angle ABC) is 30°.
- The angle at C (angle ACB) is 60°.
- The angle at A (angle BAC) can be calculated as:
Angle A=180°−(30°+60°)=90°
This confirms that triangle ABC is a right triangle with angle A being the right angle.
Step 4: Apply Trigonometric Ratios
In a right triangle, we can use the tangent function to find the height (breadth of the canal). The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side.
1. For angle ABC (30°):
tan(30°)=heightBC
Here, BC = 100 meters.
tan(30°)=height100
We know that tan(30°)=1√3:
1√3=height100
Thus, the height (h) is:
h=100√3≈57.74 meters
2. For angle ACB (60°):
tan(60°)=heightAB
Here, we can use the relationship between the sides:
tan(60°)=√3=heightAB
Rearranging gives:
height=AB⋅√3
Step 5: Solve for the Height
Using the 30-60-90 triangle properties:
- The side opposite the 30° angle (height) is half the hypotenuse (BC).
- The side opposite the 60° angle is √32 times the hypotenuse.
Thus, we can calculate the height (breadth of the canal):
height=100⋅12⋅√3=50√3
Final Answer
The breadth of the canal is:
Breadth=50√3 meters
We have a canal with two banks that are parallel. Points A, B, and C represent three persons, where A is on one bank and B and C are on the opposite bank. The angles given are:
- Angle ABC = 30°
- Angle ACB = 60°
From the information given, we can form triangle ABC. The sides of the triangle are:
- BC = 100 meters (the distance between B and C)
- We need to find the height (the breadth of the canal), which is the perpendicular distance from point A to line BC.
In triangle ABC:
- The angle at B (angle ABC) is 30°.
- The angle at C (angle ACB) is 60°.
- The angle at A (angle BAC) can be calculated as:
Angle A=180°−(30°+60°)=90°
This confirms that triangle ABC is a right triangle with angle A being the right angle.
In a right triangle, we can use the tangent function to find the height (breadth of the canal). The tangent of an angle in a right triangle is the ratio of the opposite side to the adjacent side.
tan(30°)=heightBC
Here, BC = 100 meters.
tan(30°)=height100
We know that tan(30°)=1√3:
1√3=height100
Thus, the height (h) is:
h=100√3≈57.74 meters
tan(60°)=heightAB
Here, we can use the relationship between the sides:
tan(60°)=√3=heightAB
Rearranging gives:
height=AB⋅√3
Using the 30-60-90 triangle properties:
- The side opposite the 30° angle (height) is half the hypotenuse (BC).
- The side opposite the 60° angle is √32 times the hypotenuse.
height=100⋅12⋅√3=50√3
The breadth of the canal is:
Breadth=50√3 meters
Topper's Solved these Questions
Similar Questions
Knowledge Check
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is 60∘ . when he returns 40 m from the bank, he finds the angle to be 30∘. What is the breadth of the river?
A40 mB60 mC20 mD30 mA person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60∘. When he retreats 40 m from the bank, he finds the angle to be 30∘.The breadth of the river is
A20mB40mC30mD60mA person standing on the bank of a river observes that the angle subtended by a tree on the opposite of bank is 60∘. When he retires 40 m.from the bank, he finds the angle to be 30∘. What is the breadth of the river ?
A60mB40mC30mD20m
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60∘, when he retreats 40m from the bank he finds the angle to be 30∘. Find the height of the tree and the breadth of the river.
View SolutionA person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60∘, when he retires 14 m from the bank, he finds the angle to be 30∘. Find the height of the tree and the breadth of the river.
View SolutionA person standing on the bank of a river observers that the angle subtends by a tree on the opposite bank is 60∘. When he retires 40 feet from the bank, he finds the angle to be 30∘. Find the height of the tree and the breadth of the river.
View SolutionA person, standing on the bank of a river, observes that the angle subtended by a tree on the opposite bank is 600. When he retreates 20m from the bank, he finds the angle to be 300. Find the height of the tree and the breadth of the river.
View SolutionIf A, B and C are the interior angles of triangle ABC, find tan(B+C2)
View Solution