In a triangle ABC. AC = 5 cm, AB = 7 cm, BC=√39 what is the measure of angle A ? is the measure of angle A ?
45∘
60∘
90∘
30∘
The correct Answer is:B
To find the measure of angle A in triangle ABC where AC = 5 cm, AB = 7 cm, and BC = √39 cm, we can use the cosine rule. The cosine rule states:
cosA=b2+c2−a22bc
Where:
- a is the side opposite angle A (BC),
- b is the side opposite angle B (AC),
- c is the side opposite angle C (AB).
In our case:
- a=√39 (BC),
- b=5 (AC),
- c=7 (AB).
Step 1: Substitute the values into the cosine rule formula
cosA=52+72−(√39)22⋅5⋅7
Step 2: Calculate 52, 72, and (√39)2
52=25
72=49
(√39)2=39
Step 3: Substitute these values back into the formula
cosA=25+49−392⋅5⋅7
Step 4: Simplify the numerator
25+49=74
74−39=35
Step 5: Calculate the denominator
2⋅5⋅7=70
Step 6: Substitute the simplified numerator and denominator
cosA=3570
Step 7: Simplify the fraction
cosA=12
Step 8: Find the angle A
The angle whose cosine is 12 is 60∘.
Conclusion
Thus, the measure of angle A is 60∘.
---
- a is the side opposite angle A (BC),
- b is the side opposite angle B (AC),
- c is the side opposite angle C (AB).
- a=√39 (BC),
- b=5 (AC),
- c=7 (AB).
72=49
(√39)2=39
74−39=35
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES Book:PUNEET DOGRAChapter:PROPERTIES OF TRIANGLES Exercise:PREV YEAR QUESTION
Explore 30 Videos
- PROBABILITYBook:PUNEET DOGRAChapter:PROBABILITYExercise:PREV YEAR QUESTIONS
Explore 159 Videos
- QUADRATIC EQUATIONSBook:PUNEET DOGRAChapter:QUADRATIC EQUATIONSExercise:PREV YEAR QUESTIONS
Explore 103 Videos
Similar Questions
In a triangle ABC, AB=6 √3 cm, AC = 12 cm and BC =6cm . Then measure of ∠B is equal to :
एक त्रिभुज ABC में, AB=6 √3 cm, AC = 12 cm और BC = 6cm| ∠B का माप ज्ञात करे
View SolutionIn △ABC, AB=7 cm, BC = 10 cm, and AC = 8 cm. If AD is the angle bisector of ∠BAC , where D is a point on BC, then BD is equal to:
View Solution
Knowledge Check
In a triangle ABC, BC = √39, AC = 5 and AB = 7. What is the measure of the angle A?
Aπ4Bπ3Cπ2Dπ6In a △ABC. AB = 5 cm, AC = 7 cm. If AD is the angle bisector of angle A, then BD :CD is :
A25:49B49:25C6:1D5:7If the angles of a triangle ABC are in AP and b:c=√3:√2 the what is the measure of angle A?
AA. 30∘BB. 45∘CC. 60∘DD. 75∘
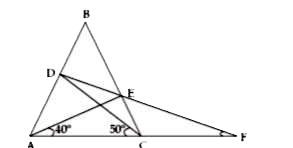
The given figure shows an isosceles triangle ABC with AB = BC and angle B = 20∘. Points D&E are on AB & BC respectively so that the measure of angle CAE is 40∘ degrees and the measure of angle ACD is 50∘ degrees. DE and AC meet at F. Find the measure of angle AFD.
View SolutionIn a triangle ABC, if AB = BC and the measure of angle C is 75∘, then the measure of angle B is:
View SolutionIn ΔABC,AB=6√3cm,AC=12cm,BC=6cm. Find measure of ∠A.
View SolutionIn a right -angled triangle ABC, ∠ABC=90∘,AB=5cm and BC = 12 cm . The radius of t he circumcircle of the triangle ABC is
View SolutionIn △ABC, if AB=AC and ∠BAC=40∘ ,then the measure of ∠B is
त्रिभुज ABC में, यदि AB=AC है तथा ∠BAC=40∘ है, तो कोण B का मान क्या होगा ?
View Solution