Question

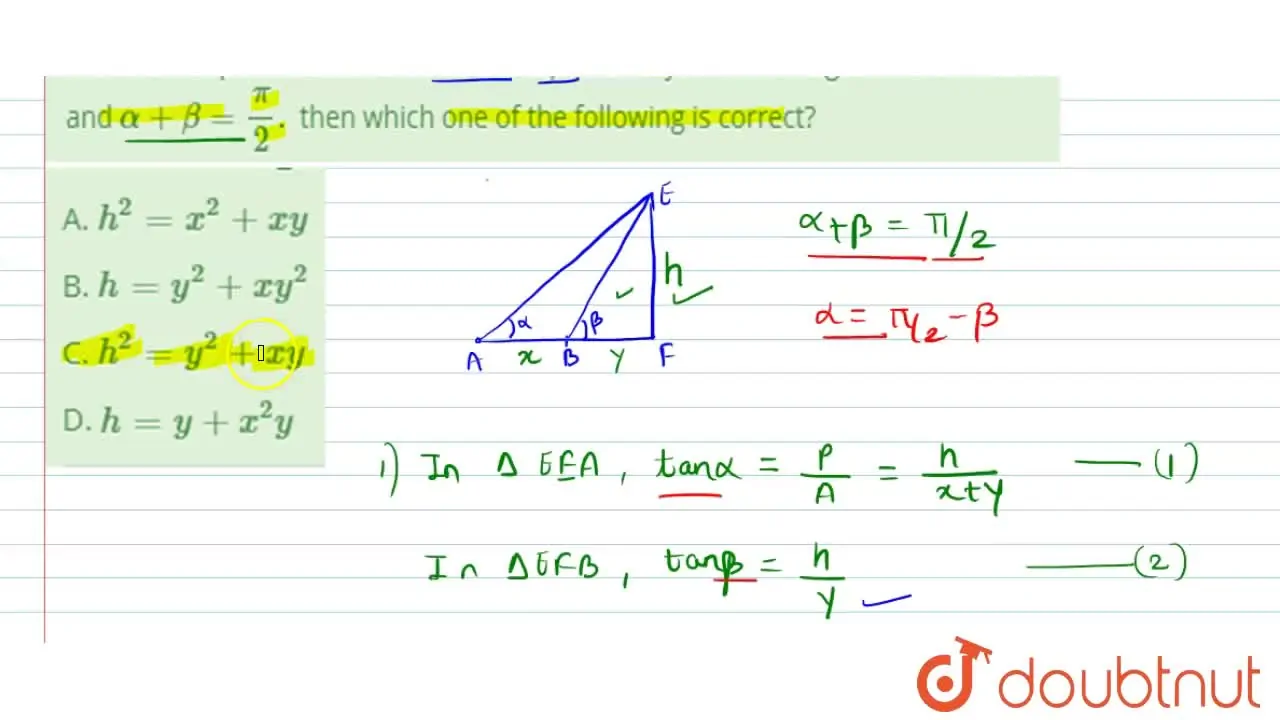
The angle of elevation of the top of a tower EF ( F being the foot of the tower) as seen from a point A which is on the same level as F. is a. On advancing towards the foot of the lower the angle of elevation of the top of the tower as seen from a point B such that AB = x. is $\beta$. If BF = y. h is the height of the tower and $\alpha +\beta =\frac{\pi }{2}.$ then which one of the following is correct?

Options

A. A. `h ^(2 ) = x ^(2) + xy`
B. B. `h = y ^(2) + xy ^(2)`
C. C. ` h^ 2 = y ^(2) + xy`
D. D. `h = y + x ^(2) y `

Answer

C

Explanation

To solve the problem step by step, we will analyze the given information and derive the necessary equations.

Step 1: Understand the Problem
We have a tower EF with F being its foot. The angle of elevation from point A to the top of the tower E is α, and from point B (which is closer to the tower) to E is β. We know that the distance AB = x and BF = y. The height of the tower is h, and we have the relationship α + β = π/2.

Step 2: Draw the Diagram
Let's visualize the situation:
- Draw a vertical line representing the tower EF.
- Mark point F at the bottom (foot of the tower) and point E at the top.
- Mark point A at a distance from F where the angle of elevation to E is α.
- Mark point B closer to F where the angle of elevation to E is β.
- Label the distances: AB = x and BF = y.

Step 3: Set Up the First Triangle (EAF)
In triangle EAF:
- The height of the tower (EF) is h.
- The horizontal distance from A to F is (x + y).
- By the definition of tangent in a right triangle:

\( \tan(\alpha) = \frac{h}{x + y} \)

Step 4: Set Up the Second Triangle (EFB)
In triangle EFB:
- The height of the tower (EF) is still h.
- The horizontal distance from B to F is y.
- Again, by the definition of tangent:

\( \tan(\beta) = \frac{h}{y} \)

Step 5: Use the Relationship Between Angles
Since α + β = π/2, we can express α in terms of β:

\( \alpha = \frac{\pi}{2} - \beta \)

Using the identity for tangent:

\( \tan\left(\frac{\pi}{2} - \beta\right) = \cot(\beta) \)

Thus, we can rewrite the first equation:

\( \cot(\beta) = \frac{h}{x + y} \)

Step 6: Relate the Two Equations
Now we have two equations:
1. \(\tan(\beta) = \frac{h}{y}\)
2. \(\cot(\beta) = \frac{h}{x + y}\)

From the second equation, we can express cotangent in terms of tangent:

\( \cot(\beta) = \frac{1}{\tan(\beta)} \)

Step 7: Multiply the Two Equations
Now we multiply the two equations:

\( \tan(\beta) \cdot \cot(\beta) = \frac{h}{y} \cdot \frac{h}{x + y} \)

Since \(\tan(\beta) \cdot \cot(\beta) = 1\), we have:

\( 1 = \frac{h^2}{y(x + y)} \)

Step 8: Rearranging the Equation
Rearranging gives us:

\( h^2 = y(x + y) \)

Expanding this:

\( h^2 = xy + y^2 \)

Step 9: Final Relation
This can be rearranged to:

\( x^2 = y^2 + xy \)

Conclusion
Thus, the correct relation derived from the problem is:

\( x^2 = y^2 + xy \)