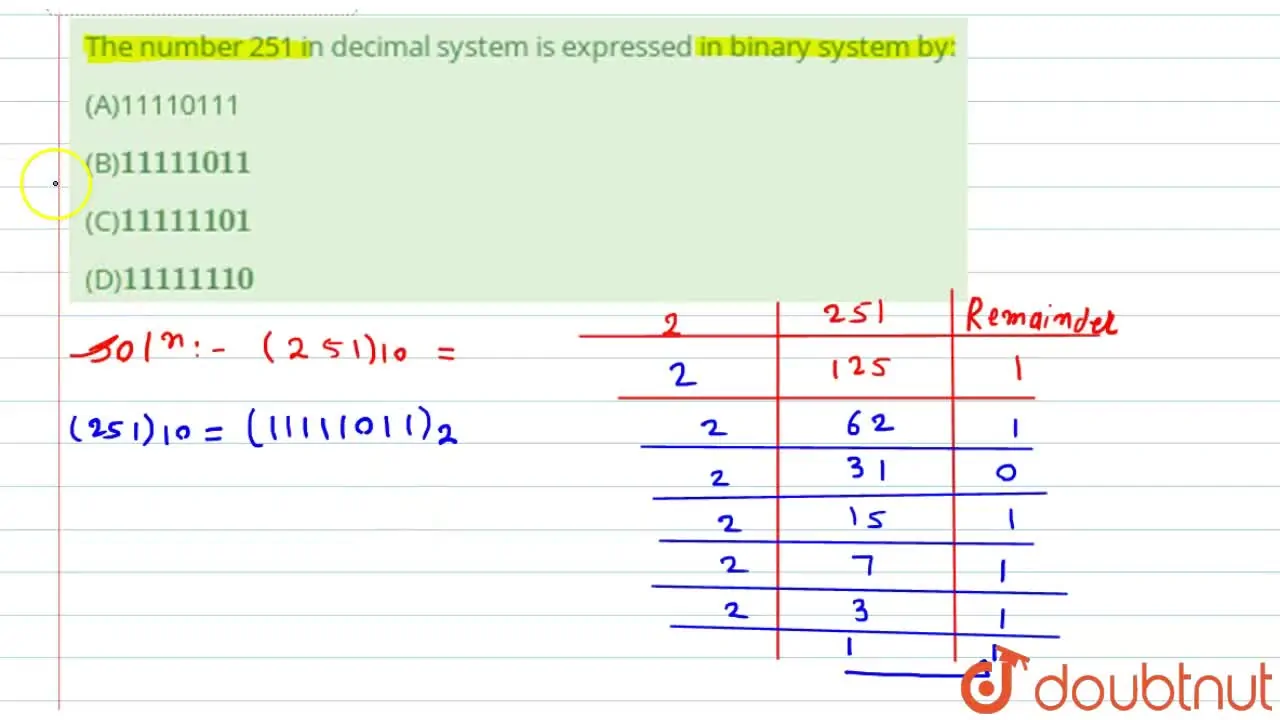
The number 251 in decimal system is expressed in binary system by:
(A)11110111
(B)11111011
(C)11111101
(D)11111110
The correct Answer is:B
Step by step video, text & image solution for The number 251 in decimal system is expressed in binary system by: by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
- BOOK - PUNEET DOGRACHAPTER - BINARY NUMBEREXERCISE - PREV YEAR QUESTIONS27videos
BINARY NUMBER
- BOOK - PUNEET DOGRACHAPTER - AREA BOUNDED BY CURVESEXERCISE - PREV YEAR QUESTIONS39videos
AREA BOUNDED BY CURVES
- BOOK - PUNEET DOGRACHAPTER - BINOMIAL THEOREMEXERCISE - PREV YEAR QUESTIONS41videos
BINOMIAL THEOREM
Similar Questions
The number 292 in decimal system is expressed in binary system by
View SolutionThe number 292 in decimal system is expressed in binary system by:
View SolutionIf the number 235 in decimal system is converted into binary system, then what is the resulting number ?
View SolutionIf the number 235 in decimal system is converted into binary system, then what is the resulting number?
View Solution56 in binary system is ?
View SolutionA number of decimal system when represented in binary system then its first and last digits are same and the rest digits are also of another kind. Further this number appears to be palindrome of numerals. The numbers is :
View SolutionThe maximum three digit integer in the decimal system will be represented in the binary system by which one of the following ?
View SolutionThe maximum three digit integer in the decimal system will be represented in the binary system by which one of the following?
View SolutionThe number 0.0011 in binary system represents
View SolutionThe difference of two numbers 10001100 and 1101101 in binary system is expressed in decimal system by which one of the following?
View Solution