6 equidistant vertical lines are drawn on a board. 6 equidistant horizontal lines are also drawn on the board cutting the 6 vertical lines, and the distance between any two consecutive horizontal lines is equal to that between any two consecutive vertical lines. What is the maximum number of squares thus formed?
A) 37
B) 55
C) 91
D) 225
The correct Answer is:C
To solve the problem of finding the maximum number of squares formed by 6 equidistant vertical lines and 6 equidistant horizontal lines, we can follow these steps:
Step 1: Understand the Grid Formation
We have 6 vertical lines and 6 horizontal lines. The intersection of these lines forms a grid. Each square is formed by selecting two vertical lines and two horizontal lines.
Step 2: Count the Squares of Different Sizes
We can form squares of various sizes within this grid. The sizes of squares we can form are:
- 1x1 squares
- 2x2 squares
- 3x3 squares
- 4x4 squares
- 5x5 squares
Step 3: Calculate the Number of Each Size of Square
1. 1x1 Squares:
- The number of 1x1 squares is determined by the number of ways to choose 2 vertical lines and 2 horizontal lines from the 6 lines.
- The number of 1x1 squares = (6 - 1) * (6 - 1) = 5 * 5 = 25.
2. 2x2 Squares:
- The number of 2x2 squares = (6 - 2) * (6 - 2) = 4 * 4 = 16.
3. 3x3 Squares:
- The number of 3x3 squares = (6 - 3) * (6 - 3) = 3 * 3 = 9.
4. 4x4 Squares:
- The number of 4x4 squares = (6 - 4) * (6 - 4) = 2 * 2 = 4.
5. 5x5 Squares:
- The number of 5x5 squares = (6 - 5) * (6 - 5) = 1 * 1 = 1.
Step 4: Sum All the Squares
Now, we sum all the squares calculated:
- Total squares = 25 (1x1) + 16 (2x2) + 9 (3x3) + 4 (4x4) + 1 (5x5) = 55.
Conclusion
The maximum number of squares that can be formed is 55.
We have 6 vertical lines and 6 horizontal lines. The intersection of these lines forms a grid. Each square is formed by selecting two vertical lines and two horizontal lines.
We can form squares of various sizes within this grid. The sizes of squares we can form are:
- 1x1 squares
- 2x2 squares
- 3x3 squares
- 4x4 squares
- 5x5 squares
- The number of 1x1 squares is determined by the number of ways to choose 2 vertical lines and 2 horizontal lines from the 6 lines.
- The number of 1x1 squares = (6 - 1) * (6 - 1) = 5 * 5 = 25.
- The number of 2x2 squares = (6 - 2) * (6 - 2) = 4 * 4 = 16.
- The number of 3x3 squares = (6 - 3) * (6 - 3) = 3 * 3 = 9.
- The number of 4x4 squares = (6 - 4) * (6 - 4) = 2 * 2 = 4.
- The number of 5x5 squares = (6 - 5) * (6 - 5) = 1 * 1 = 1.
Now, we sum all the squares calculated:
- Total squares = 25 (1x1) + 16 (2x2) + 9 (3x3) + 4 (4x4) + 1 (5x5) = 55.
The maximum number of squares that can be formed is 55.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - PRACTICE EXERCISES ( EXPERT LEVEL )
48 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - TEST YOURSELF
15 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - DISHA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - PRACTICE EXERCISES ( FOUNDATION LEVEL)
59 Videos
- PERCENTAGESBOOK - DISHA PUBLICATIONCHAPTER - PERCENTAGESEXERCISE - PRACTICE EXERCISE (TEST YOURSELF)
15 Videos
- PROBABILITYBOOK - DISHA PUBLICATIONCHAPTER - PROBABILITYEXERCISE - TEST YOURSELF
15 Videos
Similar Questions
m equi spaced horizontal lines are intersection by n equi spaced vertical lines. If the distance between two successive horizontal lines is same as that between two successive vertical lines, then find the number of squares formed by lines if (m
View Solutionm equi spaced horizontal lines are inersected by n equi spaced vertical lines. If the distance between two successive horizontal lines is same as that between two successive vertical lines, then find the number of squares formed by the lines if (m<n)
View Solution
Knowledge Check
If spheres of radius 'r' are arranged in ccp fashion (ABC ABC…) the vertical distance between any two consecutive A layers is
A4r√23B4r√32C6 rDr√6If spheres of radius 'r' are arranged in ccp fashion (ABC ABC…) , the vertical distance between any two consecutive A layers is
A4r√23B4r√32C6 rDr√6
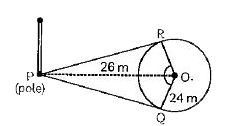
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.
View SolutionFind the distance between the two lines x+y=2 and 2x+2y=6.
View SolutionThe line graph shows the scores of a batsman in 6 consecutive matches. What is the range of his scores?

View SolutionShortest distance between two skew lines in vector + cartesian form
View SolutionShortest distance between two parallel lines in vector + cartesian form
View SolutionThe set of points joining which are equidistant from any two intersecting lines is called
View Solution
