The diagonals AC and BD of a rhombus intersect at (5, 6). If A (3, 2) then equation of diagonal BD is
y - x = 1
2 y - x = 17
y - 2x + 4 = 0
2y + x = 17
The correct Answer is:D
To find the equation of diagonal BD of a rhombus where the diagonals intersect at point (5, 6) and point A is given as (3, 2), we can follow these steps:
Step 1: Identify the coordinates of the intersection point and point A
The intersection point of the diagonals AC and BD is given as O(5, 6). Point A is given as A(3, 2).
Step 2: Find the slope of line AO
To find the slope (m1) of line AO, we use the slope formula:
m1=y2−y1x2−x1
Substituting the coordinates of points A(3, 2) and O(5, 6):
m1=6−25−3=42=2
Step 3: Determine the slope of line BD
Since the diagonals of a rhombus are perpendicular to each other, the slope of line BD (m2) can be found using the relationship:
m1⋅m2=−1
Substituting m1:
2⋅m2=−1⟹m2=−12
Step 4: Use point-slope form to find the equation of line BD
We can use the point-slope form of the equation of a line:
y−y1=m(x−x1)
Here, we will use point O(5, 6) and the slope m2 = -\frac{1}{2}:
y−6=−12(x−5)
Step 5: Simplify the equation
Expanding the equation:
y−6=−12x+52
Adding 6 to both sides:
y=−12x+52+6
Converting 6 to a fraction:
y=−12x+52+122=−12x+172
Step 6: Rearranging to standard form
To express the equation in standard form (Ax + By + C = 0):
12x+y−172=0
Multiplying through by 2 to eliminate the fraction:
x+2y−17=0
Final Answer
The equation of diagonal BD is:
x+2y−17=0
The intersection point of the diagonals AC and BD is given as O(5, 6). Point A is given as A(3, 2).
To find the slope (m1) of line AO, we use the slope formula:
m1=y2−y1x2−x1
Substituting the coordinates of points A(3, 2) and O(5, 6):
m1=6−25−3=42=2
Since the diagonals of a rhombus are perpendicular to each other, the slope of line BD (m2) can be found using the relationship:
m1⋅m2=−1
Substituting m1:
2⋅m2=−1⟹m2=−12
We can use the point-slope form of the equation of a line:
y−y1=m(x−x1)
Here, we will use point O(5, 6) and the slope m2 = -\frac{1}{2}:
y−6=−12(x−5)
Expanding the equation:
y−6=−12x+52
Adding 6 to both sides:
y=−12x+52+6
Converting 6 to a fraction:
y=−12x+52+122=−12x+172
To express the equation in standard form (Ax + By + C = 0):
12x+y−172=0
Multiplying through by 2 to eliminate the fraction:
x+2y−17=0
The equation of diagonal BD is:
x+2y−17=0
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:EXPERT LEVEL
Explore 28 Videos
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:TEST YOURSELF
Explore 15 Videos
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:FOUNDATION LEVEL
Explore 65 Videos
- AVERAGESBook:DISHA PUBLICATIONChapter:AVERAGESExercise:Test Yourself
Explore 15 Videos
- FUNCTIONSBook:DISHA PUBLICATIONChapter:FUNCTIONSExercise:Test Yourself
Explore 15 Videos
Similar Questions
Knowledge Check
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax−y−1=0Bx+y−1=0Cx−y+1=0Dx+y−7=0In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax - y - 1 = 0Bx + y - 1 = 0Cx - y + 1 = 0Dx + y - 7 =0In the given figure, ABCD is a rectangle whose diagonals AC and BD intersect at 0. If ∠OAB=28∘, then ∠OBC is equal to
 A72∘B50∘C62∘D75∘
A72∘B50∘C62∘D75∘
ABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
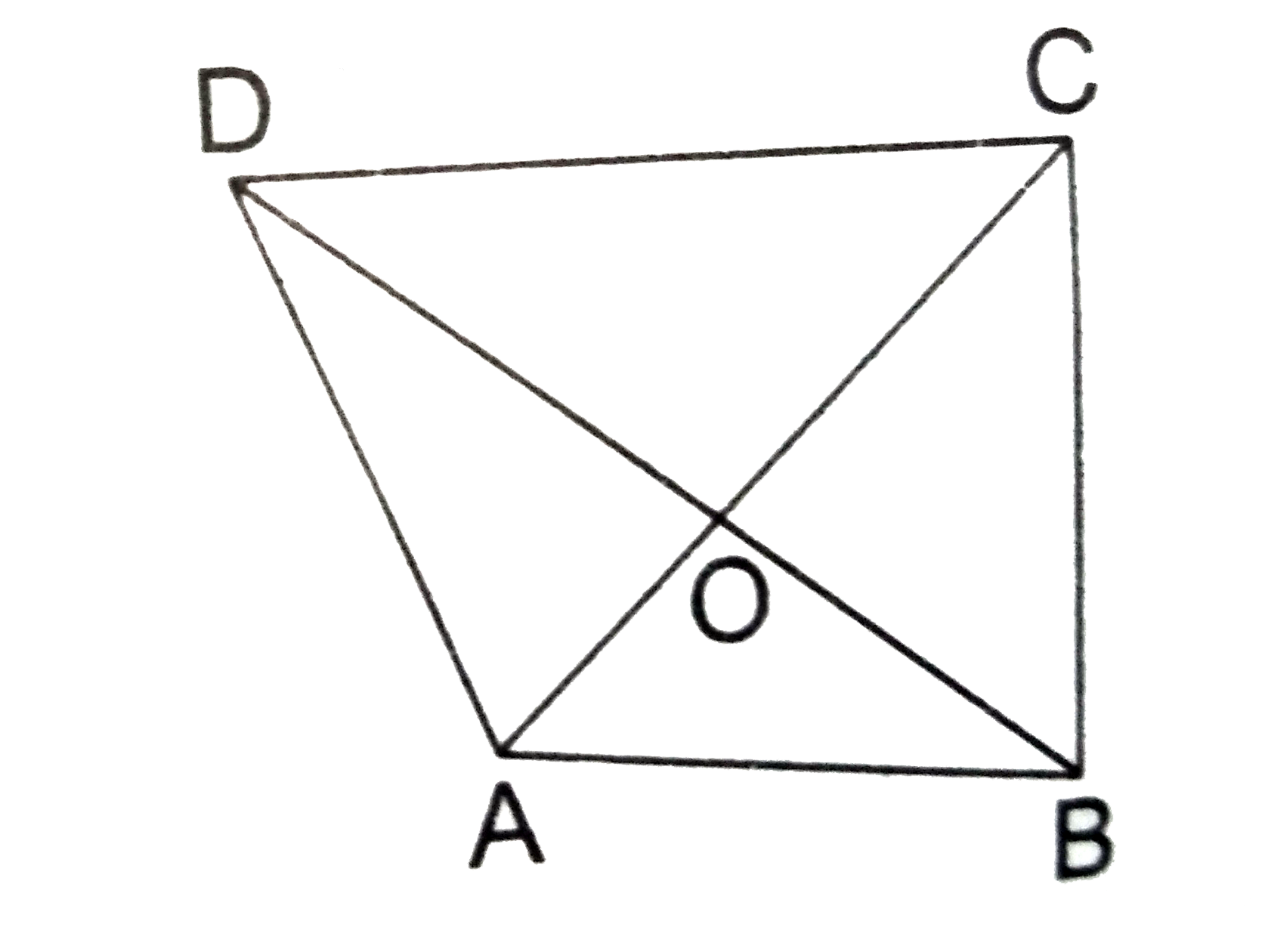
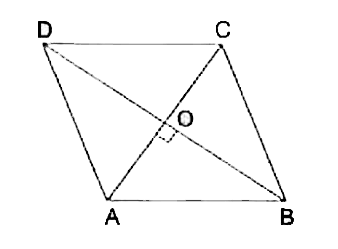
View SolutionIn the adjacent figure , ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB=10 cm and diagonal BD=16 cm , find the length of diagonal AC.
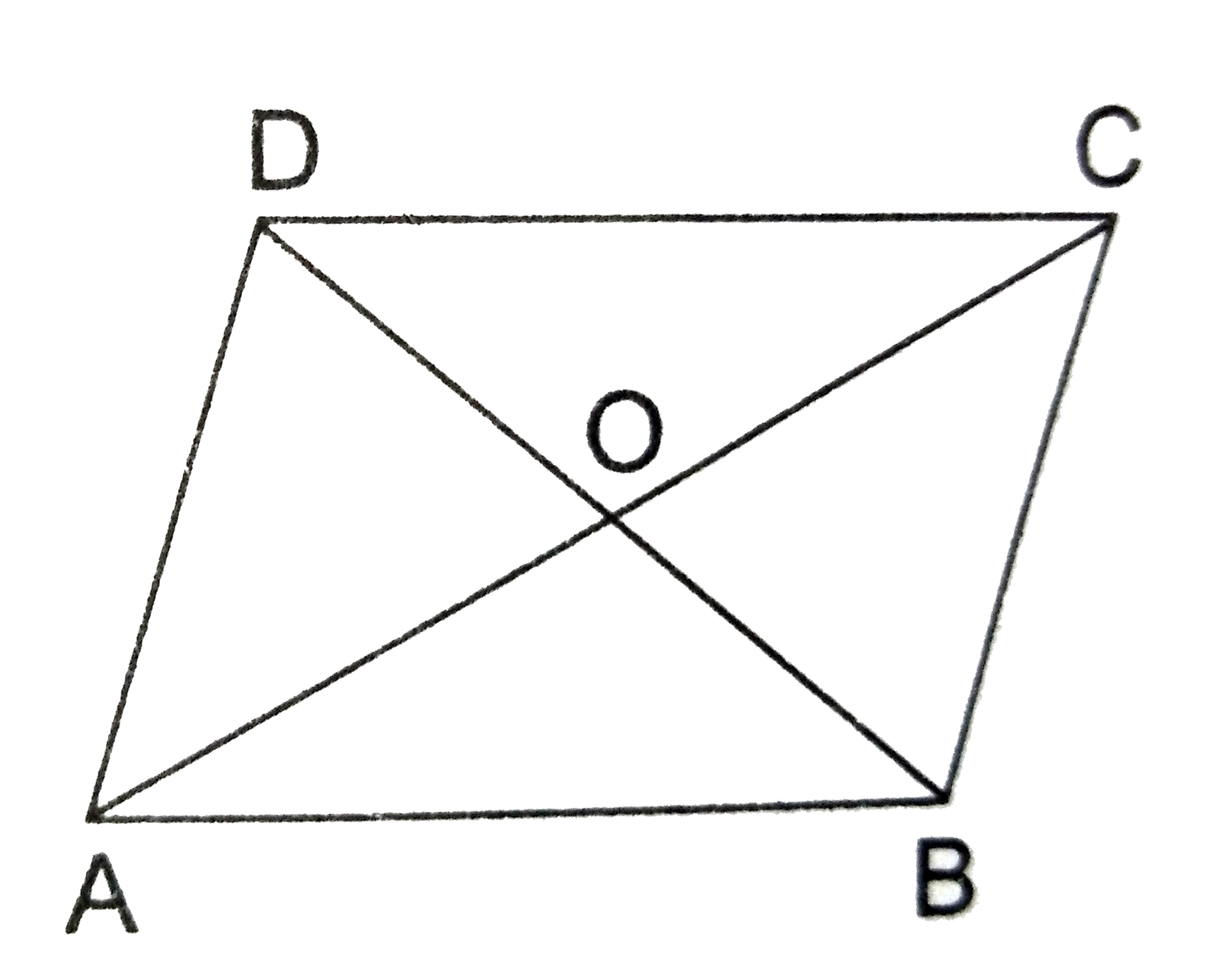
View SolutionIn the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View Solution
