If area of ' formed by joining mid-points of the sides of ΔABC is 2sq. Units. Then are of ΔABC =
(a)8
(b)4
(c)2
(d)1
8
4
2
1
The correct Answer is:A
To find the area of triangle ABC given that the area formed by joining the midpoints of its sides (triangle DEF) is 2 square units, we can follow these steps:
1. Understanding the Relationship:
When the midpoints of the sides of a triangle are joined, they form a new triangle (DEF) whose area is always 1/4 of the area of the original triangle (ABC).
2. Setting Up the Equation:
Let the area of triangle ABC be denoted as A. According to the relationship mentioned, we have:
Area of DEF=14×Area of ABC
This can be expressed mathematically as:
Area of DEF=14A
3. Substituting the Given Value:
We know from the problem that the area of triangle DEF is 2 square units. Therefore, we can substitute this value into our equation:
2=14A
4. Solving for A:
To find A, we multiply both sides of the equation by 4:
A=2×4
A=8
5. Conclusion:
Thus, the area of triangle ABC is 8 square units.
Final Answer:
The area of triangle ABC is 8 square units (Option A).
---
When the midpoints of the sides of a triangle are joined, they form a new triangle (DEF) whose area is always 1/4 of the area of the original triangle (ABC).
Let the area of triangle ABC be denoted as A. According to the relationship mentioned, we have:
Area of DEF=14×Area of ABC
This can be expressed mathematically as:
Area of DEF=14A
We know from the problem that the area of triangle DEF is 2 square units. Therefore, we can substitute this value into our equation:
2=14A
To find A, we multiply both sides of the equation by 4:
A=2×4
A=8
Thus, the area of triangle ABC is 8 square units.
The area of triangle ABC is 8 square units (Option A).
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:EXPERT LEVEL
Explore 28 Videos
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:TEST YOURSELF
Explore 15 Videos
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:FOUNDATION LEVEL
Explore 65 Videos
- AVERAGESBook:DISHA PUBLICATIONChapter:AVERAGESExercise:Test Yourself
Explore 15 Videos
- FUNCTIONSBook:DISHA PUBLICATIONChapter:FUNCTIONSExercise:Test Yourself
Explore 15 Videos
Similar Questions
Find the area of the triangle formed by joining the mid -points of the sides of the triangle ABC ,whose vertices are A(0,-1),B(2,1)andC(0,3).
View SolutionThe sides of a triangle are 3 cm, 4 cm and 5 cm. The area (in cm2) of the triangle formed by joining the mid-points of the sides of this triangle is 34 (b) 32 (c) 3 (d) 6
View Solution
Knowledge Check
For a triangle ABC,D,E,F are the mid-points of its sides. If ΔABC=24 sq. units then ΔDEFis
A4 sq. unitsB6 sq. unitsC8 sq. unitsD12 sq. unitsThe diagonal of the square field measures 50m. The area of square field is?
Aa. 1250m^2Bb. 1200m^2Cc. 1205m^2Dd. 1025m^2A triangle PQR is formed by joining the mid-points of the sides of a triangle ABC. 'o' is the circumcentre of △ABC, then for △PQR, the point 'o' is :
AincentreBcircumcentreCorthocentreDcentroid
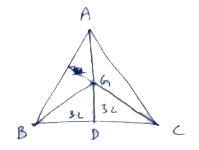
In a ΔABC,AD is median, G is a Mid point of AD. If area of ΔAGC IS 32 SQ . units then find area of ΔBGC
View SolutionIf mid-points of the sides of ΔABC are (1, 2), (0, 1) and (1, 0), then find the coordinates of the vertices of ΔABC.
View SolutionIf mid-points of the sides of ΔABC are (1, 2),(0, 1) and (1, 0), then find the coordinates of the vertices of ΔABC
View SolutionThe circumference of the circle is 176m. Then the area of the circle is:-
View SolutionThe triangle is formed by joining the mid-points of the sides AB,BC and CA of △ABCand the area of △PQR is 6cm2, then the area of △ABC is :
View Solution
